自動控制系統(tǒng)的設(shè)計--PID校正
cd=[Td/N(i),1,0]; Gc=tf(mn,cd);
G_c=feedback(G*Gc,1);
step(G_c)
end
axis([0,20,0,2])
6.5.2 Zieloger-Niclosls整定公式
Zieloger-Niclosls整定公式是一種針對帶有時延環(huán)節(jié)的一階系統(tǒng)而提出的實用經(jīng)驗公式。此時,可將系統(tǒng)設(shè)定為如下形式:
|
在實際的控制系統(tǒng)中,大量的系統(tǒng)可用此模型近似,尤其對于一些無法用機理方法進(jìn)行建模的系統(tǒng),可用時域法和頻域法對模型參數(shù)進(jìn)行整定。
(一)基于時域響應(yīng)曲線的整定
基于時域響應(yīng)的PID參數(shù)整定方法有兩種。
第一法:設(shè)想對被控對象(開環(huán)系統(tǒng))施加一個階躍信號,通過實驗方法,測出其響應(yīng)信號,如圖6-31,則輸出信號可由圖中的形狀近似確定參數(shù)k,L和T(或α),其中
α=kL/T。如果獲得了參數(shù)k,L和T(或α)后,則可根據(jù)表6-1確定PID控制器的有關(guān)參數(shù)。
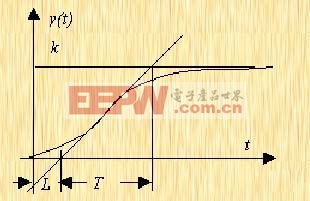 |
圖6-31 一階時延系統(tǒng)階躍響應(yīng) |

關(guān)鍵詞:
自動
控制系統(tǒng)
PID校正
相關(guān)推薦技術(shù)專區(qū)
|







評論