與頻域法相似,利用根軌跡法進(jìn)行系統(tǒng)的設(shè)計(jì)也有兩種方法:1)常規(guī)方法;2)Matlab方法。Matlab的根軌跡方法允許進(jìn)行可視化設(shè)計(jì),具有操作簡(jiǎn)單、界面直觀、交互性好、設(shè)計(jì)效率高等優(yōu)點(diǎn)。目前常用的Matlab設(shè)計(jì)方法有:1)直接編程法;2)Matlab控制工具箱提供的強(qiáng)大的Rltool工具;3)第三方提供的應(yīng)用程序,如CTRLLAB等。本節(jié)在給出根軌跡的設(shè)計(jì)思路的基礎(chǔ)上,將重點(diǎn)介紹第一、二種方法。 6.4.1 超前校正
關(guān)于超前校正裝置的用途,在頻率校正法中已進(jìn)行了較詳細(xì)的敘述,在此不再重復(fù)。 利用根軌跡法對(duì)系統(tǒng)進(jìn)行超前校正的基本前提是:假設(shè)校正后的控制系統(tǒng)有一對(duì)閉環(huán)主導(dǎo)極點(diǎn),這樣系統(tǒng)的動(dòng)態(tài)性能就可以近似地用這對(duì)主導(dǎo)極點(diǎn)所描述的二階系統(tǒng)來(lái)表征。因此在設(shè)計(jì)校正裝置之前,必須先把系統(tǒng)時(shí)域性能的指標(biāo)轉(zhuǎn)化為一對(duì)希望的閉環(huán)主導(dǎo)極點(diǎn)。通過(guò)校正裝置的引入,使校正后的系統(tǒng)工作在這對(duì)希望的閉環(huán)主導(dǎo)極點(diǎn)處,而閉環(huán)系統(tǒng)的其它極點(diǎn)或靠近某一個(gè)閉環(huán)零點(diǎn),或遠(yuǎn)離s平面的虛軸,使它們對(duì)校正后系統(tǒng)動(dòng)態(tài)性能的影響最小。 是否采用超前校正可以按如下方法進(jìn)行簡(jiǎn)單判斷:若希望的閉環(huán)主導(dǎo)極點(diǎn)位于校正前系統(tǒng)根軌跡的左方時(shí),宜用超前校正,即利用超前校正網(wǎng)絡(luò)產(chǎn)生的相位超前角,使校正前系統(tǒng)的根軌跡向左傾斜,并通過(guò)希望的閉環(huán)主導(dǎo)極點(diǎn)。 (一)根軌跡超前校正原理
設(shè)一個(gè)單位反饋系統(tǒng),G0(s)為系統(tǒng)的不變部分,Gc(s)為待設(shè)計(jì)的超前校正裝置,
Kc為附加放大器的增益。繪制G0(s)的根軌跡于圖6—19上,設(shè)點(diǎn)Sd 為系統(tǒng)希望的閉環(huán)極點(diǎn),則 若為校正后系統(tǒng)根軌跡上的一點(diǎn),必須滿足根軌跡的相角條件,即
∠Gc(Sd)G0(Sd)=∠Gc(Sd)+G0(Sd)=-π
于是得超前校正裝置提供的超前角為: 顯然在Sd已知的情況下,這樣的Gc(s)是存在的,但它的零點(diǎn)和極點(diǎn)的組合并不唯一,這相當(dāng)于張開一定角度的剪刀,以Sd為中心在擺動(dòng)。若確定了Zc和Pc的位置,即確定了校正裝置的參數(shù)。下面介紹三種用于確定超前校正網(wǎng)絡(luò)零點(diǎn)和極點(diǎn)的方法。 (二)三種確定超前校正裝置參數(shù)的方法
零極點(diǎn)抵消法 在控制工程實(shí)踐中,通常把Gc(s)的零點(diǎn)設(shè)置在正對(duì)希望閉環(huán)極點(diǎn)Sd下方的負(fù)實(shí)軸上,或位于緊靠坐標(biāo)原點(diǎn)的兩個(gè)實(shí)極點(diǎn)的左方,此法一般可使校正后系統(tǒng)的期望閉環(huán)極點(diǎn)成為主導(dǎo)極點(diǎn)。 比值α最大化法 能使超前校正網(wǎng)絡(luò)零點(diǎn)和極點(diǎn)的比值α為最大的設(shè)計(jì)方法。按照該法去設(shè)計(jì)Gc(s)的零點(diǎn)和極點(diǎn),能使附加放大器的增益盡可能地小。 以圖6—19上的點(diǎn)O和Sd,以Sd為頂點(diǎn),線段O 為邊,向左作角γ,角γ的另一邊與負(fù)實(shí)軸的交點(diǎn)Zc=-1/T,點(diǎn)Zc就是所求 的一個(gè)零點(diǎn)。再以線段ZcSd為邊,向左作角
∠PcSdZc,該角的另一邊與負(fù)實(shí)軸的交點(diǎn)Pc=-1/αT,點(diǎn) 就是所求Gc(s)的一個(gè)極點(diǎn)。根據(jù)正弦定理,由圖6—18求得: 于是有: 將夾角γ作為自變量,式(6—24)對(duì)γ求導(dǎo),并令其等于零,即dα/dγ=0
由上式解得對(duì)應(yīng)于最大α值時(shí)的γ角為 不難看出,當(dāng)希望的閉環(huán)極點(diǎn)Sd被確定后,式(6—25)中的θ和φ均為已知值,因而由上式可求得γ角,然后由式(6-22)和式(6-23)求得相應(yīng)的零極點(diǎn)。 幅值確定法 設(shè)系統(tǒng)的開環(huán)傳遞函數(shù): 且令超前校正裝置的傳遞函數(shù): 若要求校正后系統(tǒng)的穩(wěn)態(tài)誤差系數(shù)K(Kp,Kv,Ka),則由上式可首先確定k: 在開環(huán)增益k確定后,根據(jù)根軌跡原理,若Sd為校正后的閉環(huán)極點(diǎn),則它除必須滿足相角條件外,還應(yīng)滿足幅值條件: | 上式中, | 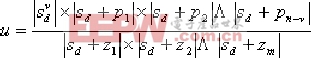 |
同樣根據(jù)平面三角形原理,對(duì)于△ZcOSd有: |
評(píng)論