自動控制系統的設計--基于根軌跡的串聯校正設計
加入技術交流群
校正后系統的閉環傳遞函數可由Matlab中的G＝feedback(Gc*G,1)得到：
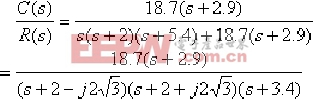
由上式可見，校正后的系統雖上升為三階系統，但由于所增加的一個閉環極點
與其零點 
靠得很近，因而這個極點對系統瞬態響應的影響就很小，從而說明了 
確為系統一對希望的閉環主導極點。由于本例題對系統的靜態誤差系數沒有提出具體的要求，故認為上述的設計是成功的。
例6－6 設一單位反饋控制系統的開環傳遞函數為
試設計一超前校正裝置，使校正后的系統能具有下列的性能指標：超調量
%，調整時間 
。
解：（1）作出校正前系統的根軌跡，如圖6—21所示。
 |
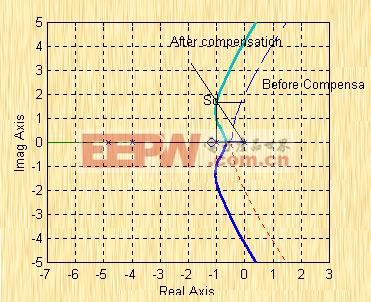| 圖6-21 |
（2）根據
，解得 
，考慮到非主導極點和零點對超調量的影響，取 
。又由 
，求得 
。進而求得系統的一對希望的閉環主導極點 
。
（3）根據求得的主導極點，計算超前校正網絡在
處應提供的超前角為
（4）由于
的開環極點正好落在希望閉環極點 
下方的負實軸上，因此可采用第一法進行校正。把 
的零點設置在緊靠 
這個開環極點的左側。如設 ，則 
的極點落在以 
為頂點，向左作角 
的負實軸交點上， 
，即為所求 
的極點。
（5） 校正后系統的傳遞函數為
由根軌跡的幅值條件，求得系統工作于 點處的K值為30.4。這樣，上式便改寫為
據此，求得校正后系統的靜態速度誤差系數
如果希望
值有少量地增大，則可通過適當調整 
零點和極點的位置來實現，但這種調整有可能會破壞 
的主導作用。
（6）它的閉環傳遞函數為：
或直接由如下的Matlab命令得到：
zpk(feedback(G0*Gc,30.4))
Zero/pole/gain:
(s+1.2)
------------------------------------------
(s+6.631) (s+1.347) (s^2 + 1.972s + 4.085)
下面檢驗希望閉環極點 
是否符合主導極點的條件。不難看出，由于閉環系統的一個極點與零點靠得很近，故它對系統瞬態響應的影響很小，同時由于另一極點 
距s平面的虛軸較遠，因而這個瞬態分量不僅幅值小，而且衰減的速度也快。由此得出，上述設計的超前校正裝置能使 
成為系統希望的閉環主導極點。
上面兩個例題均對靜態誤差系數沒有特殊要求，否則，宜采用如下方法，即第三法。
例6－7 有一單位反饋系統，其開環傳遞函數：
，設計一超前校正裝置，滿足如下性能指標：靜態誤差系數 
，閉環主導極點位于： 
處。
解：（1）繪制未校正系統的根軌跡，并根據靜態誤差系統，確定開環增益：
， 
，
（2）根據幅值確定法，并代入：
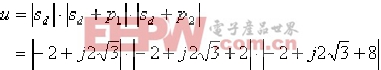
超前校正裝置應提供的超前角度：
相關推薦技術專區 |
評論