哪些運(yùn)動(dòng)方程對(duì)工業(yè)機(jī)器人很重要?
運(yùn)動(dòng)學(xué)模型是機(jī)器人運(yùn)動(dòng)的數(shù)學(xué)表示,它側(cè)重于元件之間的幾何關(guān)系,而忽略了影響運(yùn)動(dòng)的外力。運(yùn)動(dòng)學(xué)模型用于規(guī)劃和控制工業(yè)機(jī)器人的路徑。
本文引用地址:http://www.104case.com/article/202505/470498.htm正向運(yùn)動(dòng)學(xué)根據(jù)機(jī)器人手臂中每個(gè)關(guān)節(jié)的角度確定末端執(zhí)行器的當(dāng)前位置和方向。計(jì)算使用一系列變換矩陣,其中包含關(guān)節(jié)角度、長(zhǎng)度和偏移參數(shù)。
變換矩陣從機(jī)器人基礎(chǔ)到末端執(zhí)行器按順序相乘。結(jié)果是三維坐標(biāo)中的位置和末端執(zhí)行器的方向(以角度表示)。反向運(yùn)動(dòng)學(xué)反轉(zhuǎn)了該過(guò)程,根據(jù)末端執(zhí)行器的位置確定所需的關(guān)節(jié)角度,如圖 1 所示。
 圖 1.使用正向或反向運(yùn)動(dòng)學(xué)定義機(jī)器人關(guān)節(jié)位置。(圖片:MathWorks))
圖 1.使用正向或反向運(yùn)動(dòng)學(xué)定義機(jī)器人關(guān)節(jié)位置。(圖片:MathWorks))
Denavit-Hartenberg 公約
Denavit-Hartenberg (DH) 約定是表示機(jī)器人幾何和關(guān)節(jié)角度的標(biāo)準(zhǔn)化方法。它詳細(xì)介紹了如何將坐標(biāo)系附加到機(jī)器人中的關(guān)節(jié),從而定義相鄰關(guān)節(jié)之間的相對(duì)位置和方向。
如圖 2 所示,每個(gè)關(guān)節(jié)或鏈接由四個(gè)參數(shù)描述,包括鏈接長(zhǎng)度 (a)、鏈接角度 (θ)、鏈接偏移 (d) 和鏈接扭曲 (α)。這四個(gè)參數(shù)用于計(jì)算每個(gè)關(guān)節(jié)的轉(zhuǎn)換矩陣。矩陣可以相乘以確定從機(jī)器人底座到末端執(zhí)行器的整體變換。控制系統(tǒng)使用 DH 參數(shù)來(lái)計(jì)算所需的關(guān)節(jié)角度,以實(shí)現(xiàn)所需的末端執(zhí)行器姿勢(shì)。
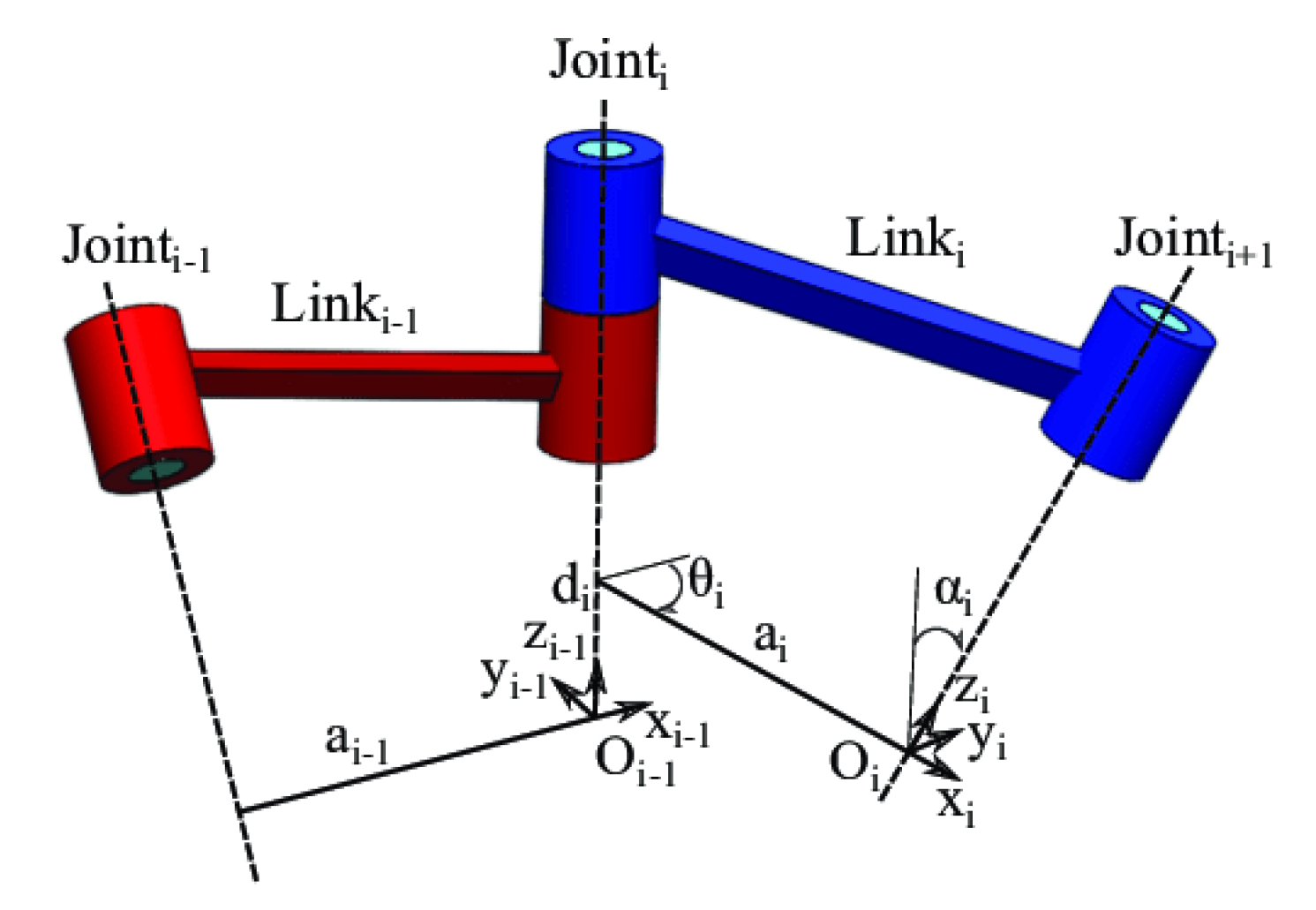 圖 2.DH 參數(shù)示例。(圖片:MDPI 傳感器)
圖 2.DH 參數(shù)示例。(圖片:MDPI 傳感器)
雅可比矩陣
DH 約定可以與雅可比矩陣一起使用,以將聯(lián)合速度與末端執(zhí)行器速度相關(guān)聯(lián)。關(guān)節(jié)速度可以描述旋轉(zhuǎn)關(guān)節(jié)的關(guān)節(jié)旋轉(zhuǎn)速度,以及棱柱關(guān)節(jié)關(guān)節(jié)的關(guān)節(jié)伸展或收縮的速度。
雅可比矩陣 (J) 是偏導(dǎo)數(shù)矩陣,用于描述關(guān)節(jié)速度和末端執(zhí)行器速度之間的關(guān)系。在機(jī)器人控制系統(tǒng)中,J 用于將關(guān)節(jié)速度映射到末端執(zhí)行器的速度。
換位 J 允許計(jì)算在末端執(zhí)行器上產(chǎn)生所需力所需的關(guān)節(jié)扭矩。在運(yùn)動(dòng)規(guī)劃中,J 用于識(shí)別和避免機(jī)器人失去自由和精確移動(dòng)能力的奇點(diǎn)。當(dāng) J 的行列式變?yōu)榱銜r(shí),就會(huì)出現(xiàn)奇點(diǎn)。
奇異
在奇點(diǎn)中,關(guān)節(jié)角度和末端執(zhí)行器位置之間的數(shù)學(xué)關(guān)系會(huì)斷開(kāi),機(jī)器人會(huì)失去一個(gè)或多個(gè)自由度。當(dāng)多個(gè)關(guān)節(jié)以阻止機(jī)器人向一個(gè)或多個(gè)方向移動(dòng)的方式對(duì)齊時(shí),就會(huì)出現(xiàn)奇點(diǎn)。這可能導(dǎo)致失控、不穩(wěn)定或動(dòng)作抽搐。通過(guò)仔細(xì)設(shè)計(jì)運(yùn)動(dòng)軌跡,可以避免奇點(diǎn)配置。
可作性
奇點(diǎn)是有限可縱性的一種形式。Manipulability (可作性) 衡量機(jī)器人根據(jù)當(dāng)前關(guān)節(jié)配置更改末端執(zhí)行器位置的程度。可縱性是使用 J 的奇異值分解來(lái)計(jì)算可縱性橢球體的。
可縱性橢球體直觀地表示機(jī)器人向不同方向移動(dòng)的能力。體積較大的橢球體表示更高的可作性。橢球體軸的比率接近 1 表示在所有方向上的可縱性相等,稱(chēng)為各向同性可縱性。較大的比率表明奇點(diǎn)正在逼近。
總結(jié)
運(yùn)動(dòng)方程用于確定從一個(gè)姿勢(shì)移動(dòng)到另一個(gè)姿勢(shì)的最佳軌跡,并避免可能限制機(jī)器人運(yùn)動(dòng)的奇點(diǎn)等困難。DH 約定是表示機(jī)器人的幾何圖形和關(guān)節(jié)角度的標(biāo)準(zhǔn)化方法。雅可比矩陣提供了用于優(yōu)化機(jī)器人運(yùn)動(dòng)的計(jì)算框架。







評(píng)論