基于Toeplitz方程的改進廣義預測PID控制
引言
PID控制技術是目前應用最廣泛的控制技術,PID控制是一種應用歷史悠久、工業界比較熟悉的簡單控制算法。自1992年Hagglund提出預測PI控制器(Hagglund,1992)的思想以來,預測PID算法得到了逐步的發展和完善,并成功的應用在一些復雜對象的控制上。控制理論由于它產生的巨大經濟效益吸引了越來越多的關注,大量的先進控制算法應用在紛繁復雜的工業過程中,也縮小了理論和實踐之間的差距。
預測算法和PID結合在一起的控制器。PID控制器和過程的滯后時間無關,而預測控制主要依賴過程的滯后時間,根據以前的控制作用,來給出現在的控制作用。而這種PID控制算法將PID的簡單性、實用性、魯棒性和模型預測控制算法的預測功能有機的結合起來了。
本文運用Toeplitz方程求解G潘圖方程,減少了預測控制計算負擔,縮短了預測控制器在線優化時間,同時解決了系統時滯引起的控制問題,整定了PID控制參數,達到了預期的效果。
問題的提出
近幾十年來,控制理論由于它產生的巨大經濟效益吸引了越來越多的關注,大量的先進控制算法應用在紛繁復雜的工業過程中,也縮小了理論和實踐之間的差距。另一方面,傳統的PID控制器,由于其簡單穩定易操作的特性,仍然在控制市場占有相當大的使用份額。所以在現今全球競爭日益激烈的市場環境下,通過先進控制改進傳統的控制器,優化傳統的控制方法來獲取經濟效益提高企業競爭力,已成為一種趨勢。
但是復雜工業過程存在著難于建模、關聯復雜、對象結構與參數時變、干擾與環境不確定、要求與約束多樣性等特點,傳統的最優控制基于對象的精確數學模型,它在工業環境中并不適用,這已為工業過程的實踐所證實,基于優化的控制顯然優于單純調節。所以就帶來了問題:如何以合適的方式將優化結合到動態控制中,形成適應于復雜工業過程的優化控制模式,預測控制就滿足了這點要求。
本研究課題將廣義預測控制和經典PID控制方法相結合,用預測優化原理解決大時滯系統的控制難題。通過對Diophantine方程快速求解,避免了傳統GPC算法中遞推求解Diophantine方程的繁雜過程。
基于Toeplitz方法改進的GPC
2.1GPC的基本表達
首先,性能指標J函數表達如下:
(1)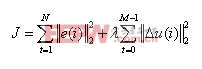
其中,e(i)是對象輸出和參考平滑曲線之間的誤差,即![]() 。N是預測時域,M是控制時域。
。N是預測時域,M是控制時域。![]() 是控制加權常數。
是控制加權常數。
可以把以上方程寫成向量形式:
(2)![]()
其中,![]() 是預測輸出誤差向量,Y是未來輸出向量,
是預測輸出誤差向量,Y是未來輸出向量,![]() 是未來控制增益向量。
是未來控制增益向量。
2.2介紹Toeplitz方程
給定一個單輸入單輸出被控對象傳遞函數模型:
(3)![]()
其中,![]() 和
和![]() 是差分后移算子的多項式:
是差分后移算子的多項式:
(4)(5)
引入增益模型:
(6)![]()
其中,![]()
引入卷積矩陣![]() 和漢克爾矩陣
和漢克爾矩陣![]() ,
,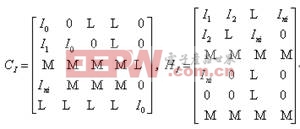
其中,![]()
所以根據![]() 和
和![]() 的定義式可以將式改寫成:
的定義式可以將式改寫成:
(7)
同理,式子右邊也可以進行變換,最后得到:




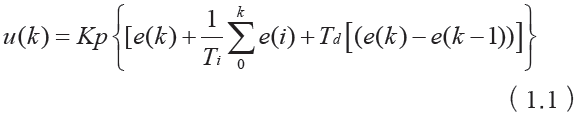

評論