基于魯棒H ∞ 控制器的磁懸浮系統(tǒng)控制設(shè)計(jì)
李亞琦,秦?斌,王?欣?(湖南工業(yè)大學(xué)?電氣與信息工程學(xué)院,湖南?株洲?412008)
本文引用地址:http://www.104case.com/article/201909/405212.htm摘?要:研究了磁懸浮小球系統(tǒng)的控制問(wèn)題,為了解決傳統(tǒng)PID控制方法在磁懸浮小球控制過(guò)程中調(diào)節(jié)效果不理想,魯棒性較差,易受外界擾動(dòng)而失去穩(wěn)定的問(wèn)題,采用了一種基于魯棒控制的方法來(lái)進(jìn)行系統(tǒng)的控制,魯棒控制算法能解決磁懸浮系統(tǒng)在外界干擾的情況下使系統(tǒng)保持預(yù)期的性能要求。將傳統(tǒng)PID控制與現(xiàn)代H ∞ 魯棒控制進(jìn)行仿真比較,通過(guò)仿真結(jié)果表明利用魯棒H ∞ 控制系統(tǒng)能夠提高磁懸浮系統(tǒng)的響應(yīng)速度,降低系統(tǒng)超調(diào)量,較少外界干擾對(duì)系統(tǒng)的影響,更好地改善了磁懸浮系統(tǒng)的動(dòng)態(tài)性能。
關(guān)鍵詞:魯棒H ∞ 控制器設(shè)計(jì);磁懸浮小球; PID;動(dòng)態(tài)性能
*文章部分由國(guó)家自然科學(xué)基金(61673166)和湖南省自然科學(xué)基金(2017JJ4022和2018JJ4070)資助。
0 引言
磁懸浮技術(shù)是一種先進(jìn)的技術(shù),現(xiàn)如今磁懸浮技術(shù)在迅猛的發(fā)展。近幾年來(lái),磁懸浮列車(chē)在我國(guó)交通運(yùn)輸中占據(jù)了重要地位,很多種磁懸浮列車(chē)模型被提出[1] 。與其他技術(shù)相比,磁懸浮技術(shù)量具有損耗低,成本低的特點(diǎn),發(fā)展這項(xiàng)技術(shù)符合我國(guó)的可持續(xù)發(fā)展戰(zhàn)略[2] 。磁懸浮系統(tǒng)是一種典型的非線性,開(kāi)環(huán)不穩(wěn)定的系統(tǒng)。磁懸浮控制算法的研究已經(jīng)引起了技術(shù)界的關(guān)注。為了更好地研究磁懸浮系統(tǒng),通過(guò)實(shí)驗(yàn)室磁懸浮小球裝置來(lái)進(jìn)行研究。對(duì)于磁懸浮小球控制算法,傳統(tǒng)的有PID控制[3] 、串級(jí)控制 [5] ,這些控制算法不能很好地滿足系統(tǒng)的動(dòng)態(tài)性能的需求。而現(xiàn)代控制算法中,魯棒控制算法 [4] 在一定程度上能夠很好地滿足系統(tǒng)的需求。
1 磁懸浮小球的工作原理及數(shù)學(xué)模型的建立
1.1 磁懸浮小球的工作原理
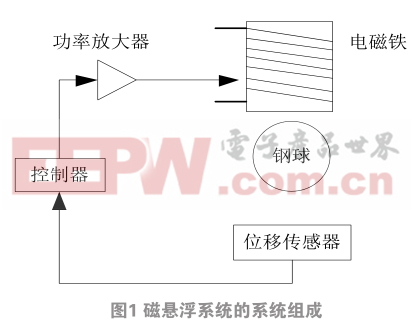
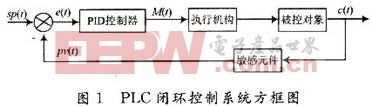
磁懸浮系統(tǒng)的組成主要包括五大部分:電磁鐵、位置傳感器、功率放大器、控制器以及被懸浮對(duì)象。系統(tǒng)組成部分如圖1所示:
磁懸浮系統(tǒng)主要是利用的電磁鐵來(lái)實(shí)現(xiàn)被懸浮對(duì)象在平衡位置的懸浮,位移傳感器主要是獲得鋼球的位置信號(hào),該信號(hào)作為控制器的輸入信號(hào)經(jīng)過(guò)控制算法計(jì)算出相應(yīng)的輸出控制信號(hào),控制器輸出的控制信號(hào)經(jīng)過(guò)功率放大器轉(zhuǎn)變成控制電流,從而使鋼球在電磁場(chǎng)中獲得磁力來(lái)保證小球處于平衡狀態(tài)。
1.2 磁懸浮系統(tǒng)的數(shù)學(xué)模型
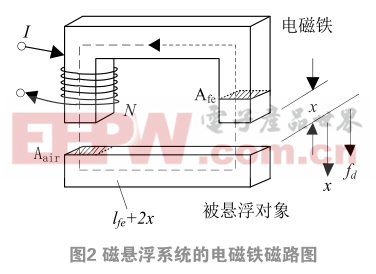
磁懸浮系統(tǒng) [9] 中的電磁力主要是通過(guò)電磁鐵采用電流勵(lì)磁方式,再配合磁懸浮小球的導(dǎo)磁特性,在空間構(gòu)成磁力線回路而產(chǎn)生的。
磁懸浮系統(tǒng)的電磁鐵磁路如圖2所示。
分析磁路,列出物理表達(dá)式:

其中

根據(jù)安培環(huán)路定理可得:
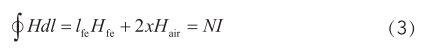
其中,N為線圈匝數(shù); I 為線圈電流;X為氣隙間距;l fe 為鐵芯回路的平均長(zhǎng)度:S(A)為鐵芯的截面積
根據(jù)式子(1)~(3)可以得到
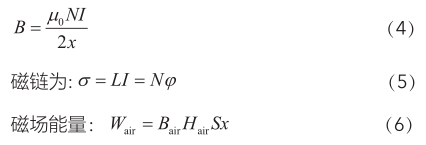
根據(jù)磁場(chǎng)能量求出電磁力:

將非線性系統(tǒng)線性化,可以得到被懸浮對(duì)象的狀態(tài)空間數(shù)學(xué)模型:
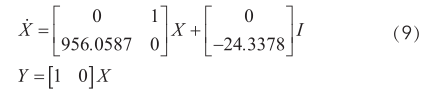
2 磁懸浮系統(tǒng)的魯棒H ∞ 控制器的設(shè)計(jì)
2.1 設(shè)計(jì)原理
魯棒控制算法 [7-8,15] 是一種現(xiàn)代控制算法,是利用這種算法設(shè)計(jì)的控制器能夠使系統(tǒng)在外界干擾的情況下還能保持穩(wěn)定性。在20世紀(jì)80年代初,Zames最先用語(yǔ)言描述了其的基本概念 [5] ,自此 H ∞ 控制器得到了迅速的發(fā)展。下文主要利用魯棒 H ∞ 控制方法來(lái)進(jìn)行磁懸浮系統(tǒng)控制器的設(shè)計(jì)。
本文進(jìn)行 H ∞ 控制器設(shè)計(jì)的時(shí)候,主要通過(guò)選擇合理的加權(quán)函數(shù)來(lái)進(jìn)行,選擇的加權(quán)函數(shù)需要滿足系統(tǒng)的動(dòng)態(tài)性能指標(biāo)以及穩(wěn)態(tài)性能指標(biāo)。 H ∞ 加權(quán)靈敏度的選擇問(wèn)題可用圖3表示:
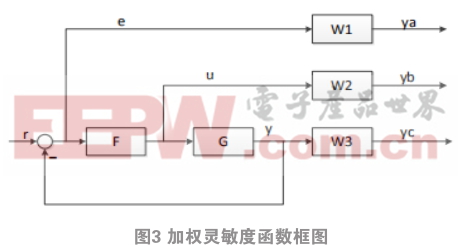
其中,r為參考輸入;e為誤差,u為控制輸入, y為輸出,y= [ya yb yc ]T,其中 W 1、W2、W3 是3個(gè)要設(shè)計(jì)的加權(quán)靈敏度函數(shù)。
定義3個(gè)傳遞函數(shù):

其中, L=GF,F(xiàn)為魯棒控制器;G為磁懸浮系統(tǒng)的開(kāi)環(huán)傳遞函數(shù);S為靈敏度。靈敏度越小意味著磁懸浮系統(tǒng)的誤差e越小;令T=I-S,定義為補(bǔ)靈敏度,T的大小直接影響著系統(tǒng)的穩(wěn)定性。在進(jìn)行控制器設(shè)計(jì)的時(shí)候,主要是權(quán)衡T與S。
2.2具體的設(shè)計(jì)步驟
在進(jìn)行磁懸浮控制系統(tǒng)設(shè)計(jì)時(shí),設(shè)計(jì)的核心是保證系統(tǒng)在增加控制器之后不僅能滿足系統(tǒng)的穩(wěn)態(tài)性能,還能使函數(shù)P的無(wú)窮范數(shù)最小。
根據(jù)加權(quán)靈敏度函數(shù)的框圖(圖3),得到 H ∞ 加權(quán)混合靈敏度 [11] 問(wèn)題的標(biāo)準(zhǔn)框架為:
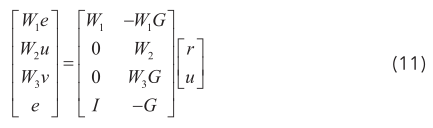
其中u=Fe。
系統(tǒng)的增廣對(duì)象模型為

令:

進(jìn)行加權(quán)函數(shù)選擇時(shí),需要滿足以下要求:
1)W 1 函數(shù)的選擇要求
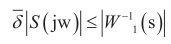 也就是 W 1 要有低通濾波特性,根據(jù)磁懸浮實(shí)際的系統(tǒng)分析,系統(tǒng)干擾一般發(fā)生在低頻段,為了更好地保證系統(tǒng)魯棒性,要使S的增益加大,同時(shí)還要保證 W 1 的截止頻率 ω 1 小于 W 3 的截止頻率 ω 3 。
也就是 W 1 要有低通濾波特性,根據(jù)磁懸浮實(shí)際的系統(tǒng)分析,系統(tǒng)干擾一般發(fā)生在低頻段,為了更好地保證系統(tǒng)魯棒性,要使S的增益加大,同時(shí)還要保證 W 1 的截止頻率 ω 1 小于 W 3 的截止頻率 ω 3 。
2)W 2 函數(shù)的選擇
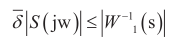 在進(jìn)行 W 2 函數(shù)選擇的時(shí)候,主要是根據(jù)控制信號(hào)(加)的大小來(lái)進(jìn)行選擇的。
在進(jìn)行 W 2 函數(shù)選擇的時(shí)候,主要是根據(jù)控制信號(hào)(加)的大小來(lái)進(jìn)行選擇的。
3)W 3 函數(shù)的選擇
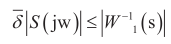 W3應(yīng)該具有高通特性,也就是上升的速率要比較大,以此來(lái)實(shí)現(xiàn)系統(tǒng)的高頻抗干擾的特性。
W3應(yīng)該具有高通特性,也就是上升的速率要比較大,以此來(lái)實(shí)現(xiàn)系統(tǒng)的高頻抗干擾的特性。
在進(jìn)行加權(quán)函數(shù)設(shè)計(jì)的時(shí)候,一般滿足以下的形式:
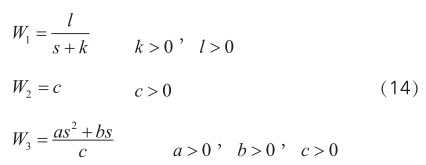
根據(jù)上述要求,選擇加權(quán)函數(shù)為:
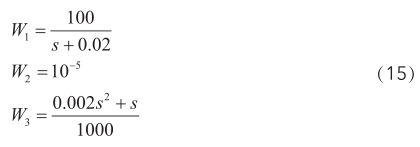
根據(jù)上述推導(dǎo),通過(guò)MATLAB命令得到系統(tǒng)魯棒控制器的傳遞函數(shù)為:
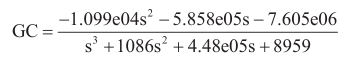
魯棒控制器的脈沖傳遞函數(shù)為:(其中采樣時(shí)間T為0.0013s)
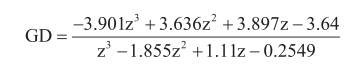
3 系統(tǒng)仿真
3.1 系統(tǒng)參數(shù)確定時(shí)的仿真
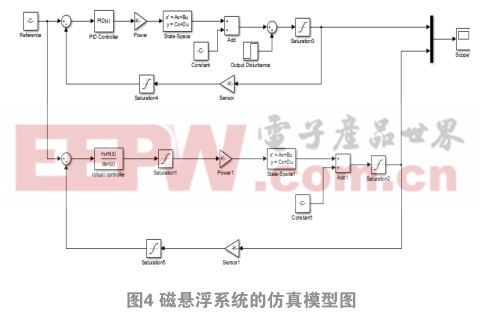
通過(guò)MATLAB/Simulink仿真模塊對(duì)系統(tǒng)進(jìn)行模型的建立與仿真。為了驗(yàn)證魯棒控制器的優(yōu)越性,將其與傳統(tǒng)的PID控制 [12-13] 進(jìn)行對(duì)比,建立的模型如圖4所示:
注釋:在進(jìn)行PID參數(shù)選擇的時(shí)候,采用臨界比例度算法,首先令K i = 0,K d = 0,令K P =1,不斷調(diào)節(jié)K p,當(dāng)Ku(kp ) = ?0.586的時(shí)候,系統(tǒng)出現(xiàn)臨界等幅震蕩,臨界震蕩的周期 T = 0.1s 。再經(jīng)過(guò)微調(diào)得出PID控制器的3個(gè)參數(shù)。
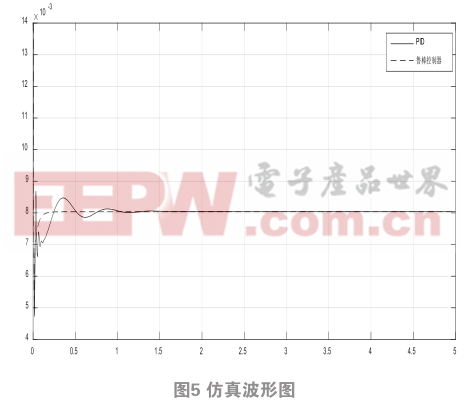
仿真結(jié)果如圖5所示:
通過(guò)上PID以及魯棒控制器仿真結(jié)果的分析與計(jì)算,得到如表1所示的指標(biāo)。
從表1可知:與傳統(tǒng)的控制器相比,應(yīng)用魯棒控制器調(diào)節(jié)時(shí)間指標(biāo)與超調(diào)量指標(biāo)都優(yōu)于PID控制器。

為了更好地驗(yàn)證魯棒控制系統(tǒng)的穩(wěn)定性,改變系統(tǒng)參數(shù)磁懸浮小球的質(zhì)量來(lái)進(jìn)行系統(tǒng)的仿真與分析:
將磁懸浮小球的質(zhì)量由46g換為40g,則系統(tǒng)的狀態(tài)方程變?yōu)?
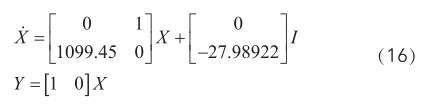
不改變PID參數(shù)以及魯棒控制器參數(shù),得到仿真波形如圖6所示。
分析仿真圖形,得到PID與魯棒控制器的動(dòng)態(tài)如表2所示。
從表2分析:當(dāng)參數(shù)發(fā)生變化的時(shí)候,魯棒控制器的動(dòng)態(tài)性能優(yōu)于PID控制器的動(dòng)態(tài)性能。
3.3系統(tǒng)外加干擾時(shí)
給系統(tǒng)在3s的時(shí)候外加一個(gè)階躍干擾信號(hào),PID控制器與魯棒控制器的仿真波形如圖7所示。

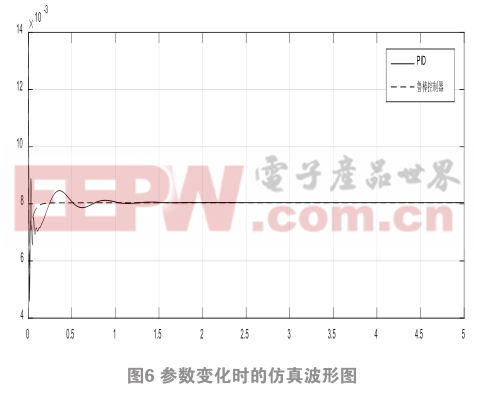
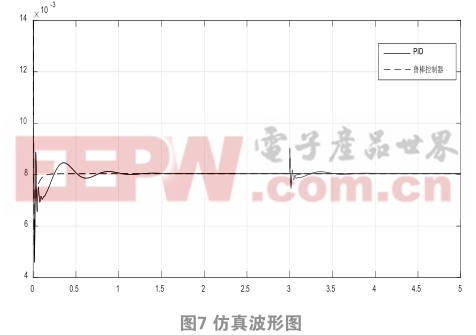
根據(jù)圖7分析,當(dāng)外加干擾的時(shí)候,魯棒控制器相對(duì)于PID控制器來(lái)講,能使系統(tǒng)在很短時(shí)間內(nèi)恢復(fù)穩(wěn)定。
4 結(jié)論
磁懸浮系統(tǒng)是一種強(qiáng)非線性,建模困難的一種系統(tǒng),并且系統(tǒng)的運(yùn)行容易受到外界環(huán)境的干擾。本文主要就這些問(wèn)題進(jìn)行了分析,對(duì)磁懸浮系統(tǒng)進(jìn)行建模,并且設(shè)計(jì)了一種 H ∞ 魯棒控制系統(tǒng)。實(shí)驗(yàn)分析表明,當(dāng)系統(tǒng)參數(shù)改變時(shí),魯棒控制器比PID控制器動(dòng)態(tài)性能更好;當(dāng)系統(tǒng)受到外界干擾時(shí),魯棒控制器系統(tǒng)也能夠迅速地回到穩(wěn)定值。
參考文獻(xiàn)
[1] MEINS J, MILLER L, Mayer W. The high speed Maglevtransportation system TRANSRAPID[J].IEEE Transactions onMagnetics,1988,24(2):808 811 ? .
[2] 王義進(jìn),席文明.磁懸浮球控制系統(tǒng)的設(shè)計(jì)研究[J].計(jì)算機(jī)測(cè)量與控制,2007,15(5):608 634 ? .
[3] 劉恒坤,郝阿明,常文森.磁懸浮系統(tǒng)的非線性PID控制[J].控制工程,2007,14(6): 653 656 ? .
[4] 趙正黎,于惠鈞,張發(fā)明,等.基于模糊 PID 控制的直流電機(jī)調(diào)速系統(tǒng)[J]. 湖南工業(yè)大學(xué)學(xué)報(bào),2015,29(2):38 43 ? .
[5] 岳婷婷,石紅瑞,曹南.基于 H = 最優(yōu)靈敏度的串級(jí)控制研究與應(yīng)用[J].石油化工自動(dòng)化.
[6] ZAMES G.Feedback and Optimal Sensitivity:Modelreference transformations, multiplicative semi-norms, andapproximate Inverse[J].IEEE Transactions on AutomaticControl,1981,36(1):301 320 ? .
[7] STEPHEN C,Paschall II.design,fabrication,and controlof a single actuator magnetic levitation system[D]. Texas A andM University Mechanical Engineering Department,2002.
[8] 曹廣忠,潘劍飛,黃蘇丹,等.磁懸浮系統(tǒng)控制算法及實(shí)現(xiàn)[M].北京:清華大學(xué)出版社,2013.
[9] 劉克平,吳建軍. H = 魯棒模糊控制在磁懸浮球系統(tǒng)中的應(yīng)用[J].長(zhǎng)春工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版),2008(4):366 370 ? .
[10] 黎恒,肖伸平.磁懸浮系統(tǒng)的滑膜變結(jié)構(gòu)魯棒控制器設(shè)計(jì)[J].湖南工業(yè)大學(xué)學(xué)報(bào),2014, 28(1):58 61 ? .
[11] 程武山.智能控制理論方法與應(yīng)用[M].北京: 清華大學(xué)出版社,2009.
[12] 劉金琨.先進(jìn)PID控制MATLAB仿真[M].北京: 電子工業(yè)出版社,2011.
[13] 張靜,馬俊麗,岳靜,等.MATLAB在控制系統(tǒng)中的應(yīng)用[M].北京:電子工業(yè)出版社,2007.
[14] Yan L.Suggestion for selection of maglev option forBeijing-Shanghai high-speed line[J].IEEE Transactions onApplied Superconductivity,2004,14(2):936 939 ? .
[15] 張士勇.磁懸浮技術(shù)的應(yīng)用與發(fā)展[J].工業(yè)儀表與自動(dòng)化裝置,2003(3):63 65 ? .
作者簡(jiǎn)介:
李亞琦(1993—),女,碩士,研究方向:人工智能。
秦斌(1963—),男,博士,教授,研究方向:智能控制,過(guò)程控制。
王欣(1971—),女,博士,教授,復(fù)雜工業(yè)過(guò)程建模與優(yōu)化控制。
本文來(lái)源于科技期刊《電子產(chǎn)品世界》2019年第10期第37頁(yè),歡迎您寫(xiě)論文時(shí)引用,并注明出處。




評(píng)論