頻率響應法--奈奎斯特穩定判據
加入技術交流群
＝2時，
剛好經過（－1，j0），系統處于臨界穩定狀態；當
＝4時，
包圍（－1，j0）點，所以閉環系統是不穩定的。可見，時滯時間的增大，對控制系統的穩定和性能都是極為不利的。 |
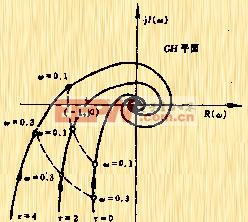| 圖5－47 |
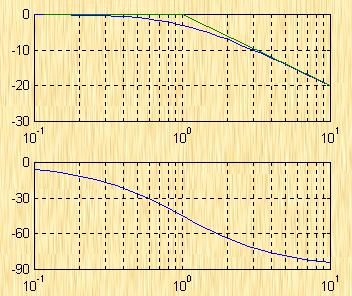
5.4.4 奈氏穩定判據在對數坐標圖上的應用
與奈氏圖的繪制相比，開環對數頻率特性的繪制更為簡單、方便，因而研究開環對數頻率特性形式的奈氏穩定判據是有實際意義的。注意到開環系統的奈氏圖與相應的對數坐標圖之間有著下列的對應關系：
1）GH平面上單位圓的圓周與對數坐標圖上的0dB線相對應，單位圓的外部對應于
，單位圓的內部對應于
。
2）GH平面上的負實軸與對數坐標圖上的
線相對應。
 |
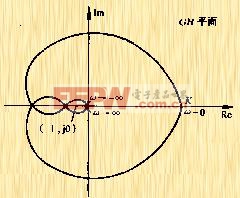| 圖5－48a 奈氏圖上正、負穿越 |
 |
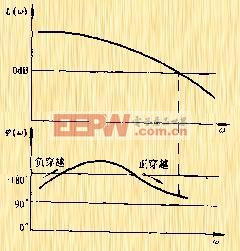| 圖5－48b 伯德圖上正、負穿越示 |
如果
曲線以逆時針方向包圍（－1，j0）點一周，則此曲線必然由上向下穿越負實軸的
線段一次。由于這種穿越使相角增大，故稱為正穿越，其次數用
表示。反這，若
曲線按順時針方向包圍（－1，j0）點一周，則此曲線將由下向上穿越負實軸的
線段一次。由于這種穿越使相角減小，故稱為負穿越，其次數用
表示。圖5－48a所示的為正負穿越數各一次的圖形。顯然，對應于圖5－48a上的正負穿越在伯德圖上表現為：在
的頻域內，當
增加時，相頻曲線
由下而上（負穿越）和由上而下（正穿越）穿過
線各一次，如圖5－48b所示。
不難看出，在極坐標圖上
曲線對于（－1，j0）點的包圍圈數N與其相頻特性曲線
在對數坐標圖上的負，正穿越數之差相等。即有
 |
|
式中
， 為在 
頻率范圍內
的負穿越數；
為在
頻率范圍內
的正穿越數。這樣，式（5－44）便可改寫為
 |
|
應用上式，就可得到對數頻率特性形式的奈奎斯特判據：閉環系統穩定的充要條件是，當
變化時，在
頻率范圍內，相率特性
穿越
線的次數（正、負穿越數之差）為
。
在使用對數頻率特性的奈氏穩定判據時，應注意如下兩點：
（1） 判據中的頻率范圍是
，而非如前述的 
；
（2） 若P為奇數，則意味著開環系統并未產生真正的穿越，即相頻特性的起點在負半軸
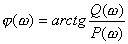
評論