頻率響應法--奈奎斯特穩定判據
![]() =常數
=常數
這說明當s沿著半徑為無窮大的半圓變化時,函數![]() 始終是一常數。由此,
始終是一常數。由此,![]() 平面上的映射曲線
平面上的映射曲線![]() 是否包圍坐標原點,只取決于奈氏軌線中
是否包圍坐標原點,只取決于奈氏軌線中![]() 部分的映射,即由
部分的映射,即由![]() 軸的映射曲線來表征。
軸的映射曲線來表征。
設在 ![]() 軸上不存在
軸上不存在![]() 的極點和零點,則當s沿著
的極點和零點,則當s沿著![]() 軸由
軸由 ![]() 運動到
運動到![]() 時,在
時,在![]() 平面上的映射曲線
平面上的映射曲線![]() 為
為
|
設閉合曲線![]() 以順時針方向包圍了
以順時針方向包圍了![]() 的z個零點和p個極點,由輻角原理可知,在
的z個零點和p個極點,由輻角原理可知,在![]() 平面上的映射曲線
平面上的映射曲線![]() 將按順時針方向圍繞著坐標原點旋轉N周,其中
將按順時針方向圍繞著坐標原點旋轉N周,其中
|
由于
因而映射曲線![]() 對其坐標原點的圍繞相當于開環頻率特征曲線
對其坐標原點的圍繞相當于開環頻率特征曲線![]() 對GH平面上的(-1,j0)點的圍繞,圖5-38示出了奈氏曲線映射在這兩個平面上的位置。
對GH平面上的(-1,j0)點的圍繞,圖5-38示出了奈氏曲線映射在這兩個平面上的位置。
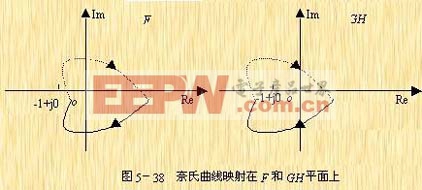 |
通過上述分析可知,閉環系統的穩定性可通過其開環頻率響應![]() 曲線對(-1,j0)點的包圍與否來判別,這就是下述的奈奎斯特穩定判據。
曲線對(-1,j0)點的包圍與否來判別,這就是下述的奈奎斯特穩定判據。
(1) 如果開環系統是穩定的,即P=0,則閉環系統穩定的充要條件是![]() 曲線不包圍(-1,j0)點。
曲線不包圍(-1,j0)點。
(2) 如果開環系統不穩定,且已知有P個開環極點在s的右半平面,則閉環系統穩定的充要條件是![]() 曲線按逆時針方向圍繞(-1,j0)點旋轉P周。
曲線按逆時針方向圍繞(-1,j0)點旋轉P周。
綜上,應用奈氏判據判別閉環系統的穩定性的具體步驟為:
(1)首先要確定開環系統是否穩定,若不穩定,則P為多少?
(2)作出奈氏曲線![]() 。具體作圖時可先畫出
。具體作圖時可先畫出![]() 從0到
從0到![]() 的一段曲線,然后以實軸為對稱軸,畫出
的一段曲線,然后以實軸為對稱軸,畫出![]() 從0到
從0到![]() 的另一段曲線,從而得到完整的奈氏曲線。
的另一段曲線,從而得到完整的奈氏曲線。
(3)計算奈氏曲線![]() 對點(-1,j0)按順時針方向的包圍圈數N。
對點(-1,j0)按順時針方向的包圍圈數N。
(4)根據輻角原理確定Z是否為零。如果Z=0,表示.閉環系統穩定;反之,![]() ,表示該閉環系統不穩定。Z的數值反映了閉環特征方程式的根在s右半平面上的個數。
,表示該閉環系統不穩定。Z的數值反映了閉環特征方程式的根在s右半平面上的個數。
例 5-5 試用奈氏判據判別閉環系統的穩定性。
系統的開環傳遞函數為
試用奈氏判據判別閉環系統的穩定性。
解:當ω由![]() 變化時,
變化時,![]() 曲線如圖5-39所示。因為
曲線如圖5-39所示。因為![]() 的開環極點為-0.5,-1,-2,在s的右半平面上沒有任何極點,即P=0,由圖5-39可知,由于奈氏曲線不包圍(-1,j0)這點,因此N=0,則Z=N+P=0。這表示該閉環系統是穩定的。
的開環極點為-0.5,-1,-2,在s的右半平面上沒有任何極點,即P=0,由圖5-39可知,由于奈氏曲線不包圍(-1,j0)這點,因此N=0,則Z=N+P=0。這表示該閉環系統是穩定的。
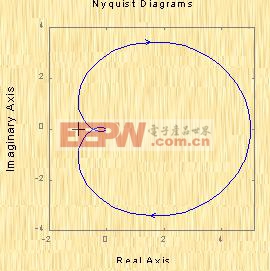 |
| 圖5-39 |
5.4.3 奈奎斯特穩定性判據的進一步說明
1、開環極點位于虛軸的情況
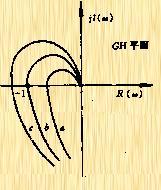
如果![]() 在虛軸上存在極點,那么就不能
在虛軸上存在極點,那么就不能



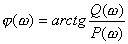


評論