前面我們從代數(shù)角度出發(fā)討論了控制系統(tǒng)穩(wěn)定性的定義和勞斯-赫爾維茨穩(wěn)定判據(jù)。本節(jié)介紹判別系統(tǒng)穩(wěn)定性的另一種判據(jù)――奈奎斯特穩(wěn)定判據(jù)。該判據(jù)是根據(jù)開(kāi)環(huán)頻率特性來(lái)判定閉環(huán)系統(tǒng)的穩(wěn)定性。同時(shí),它還能反映系統(tǒng)的相對(duì)穩(wěn)定的程度,對(duì)于不穩(wěn)定的系統(tǒng),判據(jù)與勞斯穩(wěn)定判據(jù)一樣,還能確切回答閉環(huán)系統(tǒng)有多少個(gè)不穩(wěn)定的特征根。 對(duì)于圖5-34所示的反饋控制系統(tǒng),閉環(huán)傳遞函數(shù)為:
其特征方程式為 令 將式(5-40)代入式(5-39)得 式中, 、 、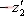 、…、 、…、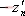 是 是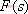 的零點(diǎn),也是閉環(huán)特征方程式的根; 的零點(diǎn),也是閉環(huán)特征方程式的根; 、 、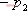 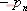 、…、 是 、…、 是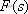 的極點(diǎn),也是開(kāi)環(huán)傳遞函數(shù)的極點(diǎn)。因此根據(jù)前述閉環(huán)系統(tǒng)穩(wěn)定的充分必要條件,要使閉環(huán)系統(tǒng)穩(wěn)定,特征函數(shù) 的極點(diǎn),也是開(kāi)環(huán)傳遞函數(shù)的極點(diǎn)。因此根據(jù)前述閉環(huán)系統(tǒng)穩(wěn)定的充分必要條件,要使閉環(huán)系統(tǒng)穩(wěn)定,特征函數(shù)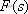 的全部零點(diǎn)都必須位于s平面的左半平面上。 的全部零點(diǎn)都必須位于s平面的左半平面上。 5.4.1 輻角原理 由于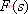 是s的有理分式,則由復(fù)變函數(shù)的理論知道, 是s的有理分式,則由復(fù)變函數(shù)的理論知道,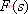 除了在s平面上的有限個(gè)奇點(diǎn)外,它總是解析的,即為單值、連續(xù)的正則函數(shù)。因而對(duì)于s平面上的每一點(diǎn),在 除了在s平面上的有限個(gè)奇點(diǎn)外,它總是解析的,即為單值、連續(xù)的正則函數(shù)。因而對(duì)于s平面上的每一點(diǎn),在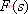 平面上必有唯一的一個(gè)映射點(diǎn)與之相對(duì)應(yīng)。同理,對(duì)s平面上任意一條不通過(guò) 平面上必有唯一的一個(gè)映射點(diǎn)與之相對(duì)應(yīng)。同理,對(duì)s平面上任意一條不通過(guò)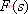 的極點(diǎn)和零點(diǎn)的閉合曲線 的極點(diǎn)和零點(diǎn)的閉合曲線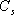 ,在 ,在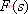 平面上必有唯一的一條閉合曲線 平面上必有唯一的一條閉合曲線 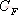 與之相對(duì)應(yīng),如圖5-35所示。若s平面上的閉合曲線 與之相對(duì)應(yīng),如圖5-35所示。若s平面上的閉合曲線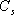 按順時(shí)針?lè)较蜻\(yùn)動(dòng),則其在 按順時(shí)針?lè)较蜻\(yùn)動(dòng),則其在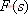 平面上的映射曲線 平面上的映射曲線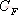 的運(yùn)動(dòng)方向可能是順時(shí)針,也可能是逆時(shí)針,它完全取決于復(fù)變函數(shù) 的運(yùn)動(dòng)方向可能是順時(shí)針,也可能是逆時(shí)針,它完全取決于復(fù)變函數(shù)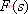 本身的特性。在此我們感興趣的不是映射曲線 本身的特性。在此我們感興趣的不是映射曲線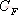 的具體形狀,而是它是否包圍 的具體形狀,而是它是否包圍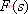 平面的坐標(biāo)原點(diǎn)以及圍繞原點(diǎn)的方向和圈數(shù),因?yàn)樗c系統(tǒng)的穩(wěn)定性有著密切的關(guān)系。 平面的坐標(biāo)原點(diǎn)以及圍繞原點(diǎn)的方向和圈數(shù),因?yàn)樗c系統(tǒng)的穩(wěn)定性有著密切的關(guān)系。 | 圖5-35 s平面上封閉曲線及其在F(s)平面上的映射線 |
圖5-35 s平面上封閉曲線及其在F(s)平面上的映射線 由式(5-41)可知,復(fù)變函數(shù)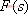 的相角為 的相角為 假設(shè)s平面上的閉合曲線計(jì)應(yīng)用文章遮罩層BEGIN-->
<div class=)

技術(shù)專區(qū)
主站蜘蛛池模板:
赤水市|
东至县|
涟源市|
阿拉善盟|
永吉县|
涞水县|
天峨县|
辽宁省|
玉田县|
湖口县|
孟村|
准格尔旗|
巫山县|
眉山市|
南郑县|
青海省|
永康市|
铜陵市|
禹城市|
宁德市|
阳信县|
鄂伦春自治旗|
来宾市|
玉林市|
武冈市|
嘉荫县|
德惠市|
千阳县|
镇江市|
历史|
祁连县|
宁安市|
岳阳市|
嘉黎县|
清水河县|
光山县|
达孜县|
合水县|
化德县|
辽源市|
庄河市|
|
評(píng)論