頻率響應法--奈奎斯特穩定判據
加入技術交流群
，因為輻角原理只適用于奈氏軌線 不通過
的奇點。為此，可對圖5－37所示的奈氏軌線作些修改，使其沿著半徑為
的半圓繞過虛軸上的所有極點。假設開環系統在坐標原點處有其極點，則對應的奈氏途徑要修改為如圖5－40所示。比較圖5－40與圖5－37可以發現，它們的區別在于圖5－40中多了一個半徑為無窮小的半圓
部分，其余兩者完全相同。因此，只需要研究圖5－40中的
部分在GH平面上的映射。 |
設系統的開環傳遞函數
 |
|
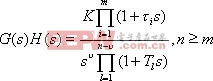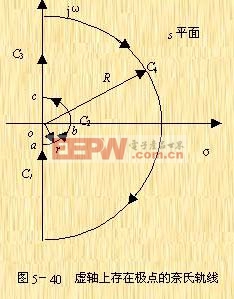
在
部分上，令
，其中
，代入上式得
 |
|
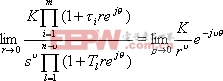當s按逆時針方向沿著
由點a移動到c時，由式（5－46）可求得其在GH平面上的映射曲線：
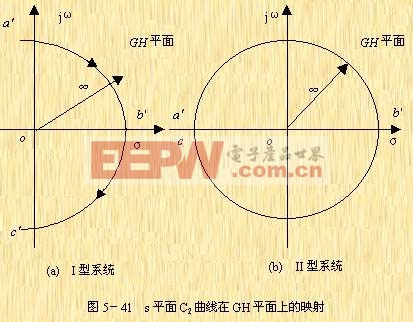
對于
的I型系統，
部分在GH平面上的映射曲線為一個半徑為無窮大的半圓，如圖5－41a所示。圖中點
、
和 
分別為
半圓上點a、b和c的映射點。
對于
的Ⅱ型系統， 部分在GH平面上的映射曲線是一個半徑為無窮大的半圓，如圖5－41b所示。
 |
把上述
部分在GH平面上的映射曲線和
的奈氏曲線在
和
處相連接，就組成了一條封閉曲線。此時，又可應用奈奎斯特穩定判據了。
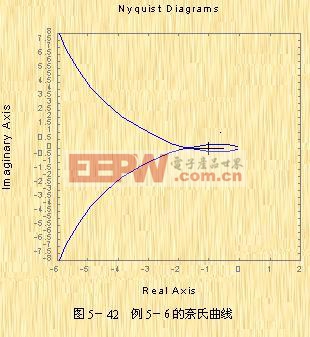
例5－6 試判別該系統的穩定性。
反饋控制系統開環傳函數為
 |
試判別該系統的穩定性。
解：由于該系統為I型系統，它在坐標原點處有一個開環極點，因而在s上所取的奈氏軌線應如圖5－40所示。該圖的
部分在GH平面上的映射曲線為一半徑為無窮大的半圓，若將它與圖5－42的奈氏曲線
相連接，則有N＝2，而系統的P＝0，因而Z＝2，即閉環系統是不穩定的，且有兩個閉環極點位于s的右半平面。
 |
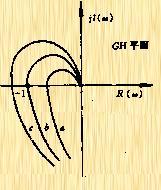
例5－7 試分析時間常數的相對大小對系統穩定性的影響并畫出它們所對應的奈氏圖。
已知系統的開環傳遞函數為
 |
試分析時間常數
和
的相對大小對系統穩定性的影響，并畫出它們所對應的奈氏圖。
解 由開環傳遞函數得
 |
 |
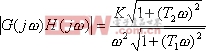根據以上兩式，作出在
，
和
三種情況下的
曲線，如圖5-43所示。當 時， 曲線不包圍（－1，j0）點，因而閉環系統穩定的。當
時，
曲線通過（－1，j0）點，說明閉環極點位于
軸上，相應的系統為不穩定的。當
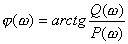
評論