控制系統的時域分析法--二階系統的暫態響應
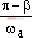 (t≥0)
(t≥0) 當ζ>1時
c(t)= (t≥0) (t≥0) |
不同ζ時單位脈沖響應曲線見圖3-10。對ζ≥1的情況,單位脈沖響應總是正值或在t=∞時為零。這時系統的單位階躍響應必是單調增長的。
由于單位脈沖響應是單位階躍響應的導數,所以單位脈沖響應曲線與時間軸第一次相交的點對應的時間必是峰值時間tp,而從t=0至t=tp這一段曲線與時間軸所包圍的面積將等于1+Mp(參見圖3-11),而且單位脈沖響應曲線與時間軸包圍的面積代數和為1。
 |
圖3-10 單位脈沖響應曲線 |
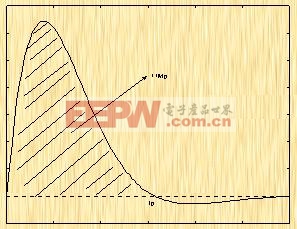 |
圖3-11 從脈沖響應求Mp |
3-10 圖示系統中 ζ=0.6,ωn =5弧度/秒。當系統受到單位階躍輸入信號作用時,試求上升時間tr、峰值時間tp、最大超調量Mp和調整時間ts。
解:根據給定的 ζ和 ωn值,可以求得ωd = ![]() =4和 σ=ζωn =3。
=4和 σ=ζωn =3。
 |
| 圖3-12 例3-10圖 |
1. 上升時間tr
上升時間為:
tr= ![]() =
= ![]()
式中β為: ![]() 弧度
弧度
因此,可求得上升時間tr為:tr= ![]() =
= ![]() 秒
秒
2. 峰值時間tp
峰值時間為:
tp= ![]() =
= ![]() =0.785秒
=0.785秒
3. 最大超調量Mp
最大超調量為:
Mp= ![]() =
= ![]() =0.095
=0.095
因此,最大超調量百分比為9.5%。
4. 調整時間ts
對于2%允許誤差標準,調整時間為:
ts= ![]() =4/3=1.33秒
=4/3=1.33秒
對于5%允許誤差標準,調整時間為:
ts= ![]() =3/3=1秒
=3/3=1秒









評論