控制系統的數學模型

在控制理論中，為了描述線性定常系統的輸入-輸出關系，最常用的函數是所謂的傳遞函數。傳遞函數的概念只適用于線性定常系統，在某些特定條件下也可以擴充到一定的非線性系統中去。

線性定常系統的傳遞函數，定義初始條件為零時，輸出量的拉普拉斯變換與輸入量的拉普拉斯變換之比。設有一線性定常系統，它的微分方程是

(2-1)

式中y是系統的輸出量，x是系統的輸入量。初始條件為零時，對方程（2-1）兩端進行拉普拉斯變換，就可以得到該系統的傳遞函數為：

(2-2)

傳遞函數是一種以系統參數表示的線性定常系統的輸入量與輸出量之間的關系式，它表達了系統本身的特性，而與輸入量無關。傳遞函數包含著聯系輸入量與輸出量所必需的單位，但它不能表明系統的物理結構（許多物理性質不同的系統，可以有相同的傳遞函數）。

傳遞函數分母中s的最高階數，就是輸出量最高階導數的階數。如果s的最高階數等于n，這種系統就叫n階系統。

例2-1 圖2-1所示為一彈簧阻尼系統，阻尼器是一種產生粘性磨擦或阻尼的裝置。它由活塞和充滿油液的缸體組成。活塞和缸體之間的任何相對運動，都將受到油液的阻滯，因為這時油液必須從活塞的一端，經過活塞周圍的間隙（或通過活塞上的專用小孔），而流到活塞的另一端。阻尼器主要用來吸收系統的能量。被阻尼器吸收的能量轉變為熱量而散失掉，而阻尼器本身不貯藏任何動能或位能。

下面來推導這一系統的傳遞函數。設系統的輸入量為外力x(t)，輸出量為質量的位移y(t)，按下列步驟進行推導：

1． 寫出系統的微分方程。
2． 假設全部初始條件等于零，取微分方程的拉普拉斯變換。
3． 求輸出Y(s)與輸入量X(s)之比。這一比值就是傳遞函數。

為了推導線性常系數微分方程，假設阻尼器的磨擦力與 成正比，并設彈簧為線性彈簧，即彈簧力與y成正比。在這個系統中，m表示質量，f表示粘性磨擦系數，而k表示彈簧剛度。
解 牛頓定律是機械系統中的基本定律。在平移系統中，牛頓定律可表示如下：

ma=ΣF=x-Fs-Ff

其中Fs=ky，

a表示加速度，f表示力。

把牛頓定律應用到這一系統可得

或

(2-3)

對方程（2-3）中每一項取拉普拉斯變換，得出

如果設初始條件等于零，即y(0)=0， (0)=0，即可得出方程（2-3）的拉普拉斯變換：

取Y(s)與X(s)之比，即可得到系統的傳遞函數：

例2-2 機械轉動系統 設有一系統，如圖2-2所示。它由慣性負載和粘性磨擦阻尼器組成。J為轉動慣量，f為粘性磨擦系數，ω為角速度，T為作用到系統上的轉矩。

解 對于機械轉動系統，其運動方程可寫成：

其微分方程為：

（2-4）

初始條件為零時，取方程（2-4）的拉普拉斯變換：

取θ(s) 與T(s)之比，即可得到系統的傳遞函數：

例2-3

圖2-3所示為一由電感L、電阻R和電容C組成。

解: 在理想條件下，可得到此電路的電壓平衡方程式：

（2-5）

由于 式中，q為電荷量，C為電容。式（2-5）可改寫為

初始條件為零時，取方程（2-5）的拉普拉斯變換：

取U(s)與Uc(s) 之比，即可得到系統的傳遞函數：

1. 系統的傳遞函數是一種數學模型，它表示聯系輸出變量與輸入變量的微分方程的一種運算方法。

2. 傳遞函數是系統本身的一種屬性，它與輸入量或驅動函數的大小和性質無關。

3. 傳遞函數包含聯系輸入量與輸出量所必需的單位，但是它不提供有關系統物理結構的任何信息（許多物理上完全不同的系統，可以具有相同的傳遞函數，稱之為相似系統）。

4. 如果系統的傳遞函數已知，則可以針對各種不同形式的輸入量研究系統的輸出或響應，以便掌握系統的性質。

5. 如果不知道系統的傳遞函數，則可通過引入已知輸入量并研究系統輸出量的實驗方法，確定系統的傳遞函數。系統的傳遞函數一旦被確定，就能對系統的動態特性進行充分描述，它不同于對系統的物理描述。

6. 用傳遞函數表示的常用連續系統有兩種比較常用的數學模型，說明如下

第一種表示方式為：

第二種表示方式也叫零極點增益模型，具體形式為：

這兩種模型各有不同的適用范圍，可以相互轉換，在不同的場合需要用不同的模型。如：在根軌跡分析中，用零極點模型就比較合適。 相似系統 相似系統這一概念，在實踐中是很有用的，因為一種系統可能比另一種系統更容易通過實驗來處理。例如，可以通過建造和研究一個與機械系統相似的電模擬系統來代替對機械系統的制造和研究，因為一般來說，電的或電子的系統更容易通過實驗進行研究。表2-1所示為相似系統的相似變量。

y=f(x) （2-6）

如果系統的額定工作狀態相應于 ，，那么方程（2-6）可以在該點附近展開成泰勒級數：

式中都在x=df/dx,d²f/dx²,… 點進行計算。如果x- 很小，可以忽略x- 的高階項。因此方程可以寫成

方程（2-8）可以改寫成

上式說明y- 與x- 成正比。方程（2-9）就是由方程（2-6）定義的非線性系統的線性數學模型。下面來研究另一種非線性系統，它的輸出量y是兩個輸入量x1和x2的函數，因而

為了得到這一非線性系統的線性近似關系，將方程（2-10）在額定工作點, 附近展開成泰勒級數。這時方程（2-10）可寫成

式中偏導數都在x₁=,x₂=上進行計算。在額定工作點附近，近似將高階項忽略。于是在額定工作狀態附近，這一非線性系統的線性數學模型可以寫成

這里介紹的線性化方法只有在工作狀態附近才是正確的。當工作狀態的變化范圍很大時，線性化方程就不合適了，這時必須使用非線性方程。應當特別注意，在分析和設計中采用的具體數學模型，只有在一定的工作條件下才能精確表示實際系統的動態特性，在其他工作條件下它可能是不精確的。

比例環節又稱放大環節，其傳遞函數為

(2-11)

這表明，輸出量與輸入量成正比，動態關系與靜態關系都一樣，不失真也不遲延，所以又稱為"無慣性環節"或"放大環節"。比例環節的特征參數只有一個，即放大系數K。工程上如無彈性變形的杠桿傳動、電子放大器檢測儀表、比例式執行機構等都是比例環節的一些實際例子。

2.4.2慣性環節

慣性環節又稱非周期環節，其傳遞函數為

(2-12)

T為慣性環節的時間常數，K為比例系數。
當輸入信號為單位階躍函數時，其環節的輸出為

它是一條指數曲線，當時間t=3T~4T時，輸出量才接近其穩態值。實際系統中，慣性環節是比較常見的，例如直流電機的勵磁回路等。

2.4.3積分環節

積分環節的傳遞函數為

(2-13)

在單位階躍輸入的作用下，積分環節的輸出c(t)為

這表明，只要有一個恒定的輸入量作用于積分環節，其輸出量就與時間成正比地無限增加。積分環節具有記憶功能，當輸入信號突然除去時，輸出總要變化下去。在控制系統設計中，常用積分環節來改善系統的穩態性能。

2.4.4微分環節

微分環節的傳遞函數為

(2-14)

理想微分環節的輸出與輸入量的變化速度成正比。在階躍輸入作用下的輸出響應為一理想脈沖（實際上無法實現），由于微分環節能預示輸出信號的變化趨勢，所以常用來改善系統的動態特性。

實際上可實現的微分環節都具有一定的慣性，其傳遞函數如下：

它有一個負極點和一個位于S平面原點的零點。實際微分環節在單位階躍輸入作用下的輸出響應為

2.4.5振蕩環節

振蕩環節的傳遞函數為

(2-15)

或

式中，T為振蕩環節的時間常數；K為放大系數；ζ為振蕩環節的阻尼比； 稱為無阻尼自然振蕩頻率。

2.4.6延遲環節

延遲環節的傳遞函數為

(2-16)

延遲環節在單位階躍輸入作用下的輸出響應為c(t)=1(t-T)

即輸出完全復現輸入，只是延遲了T時間。T為延遲環節的特征參數，稱為"延遲時間"或"滯后時間"。

以上介紹了六種典型環節，這是控制系統中最見的基本環節

方塊圖 :
系統方塊圖，是系統中每個元件的功能和信號流號的圖解表示。方塊圖表明了系統中各種元件間的相互關系。方塊圖優于純抽象的數學表達式，因為它能夠清楚地表明實際系統中的信號流動情況。

在方塊圖中，通過函數方塊，可以將所有的系統變量聯系起來。"函數方塊"或簡稱為"方塊"，是對加到方塊上的輸入信號的一種運算符號，運算結果以輸出量表示。元件的傳遞函數，通常寫進相應的方塊中，并以標明信號流向的箭頭，將這些方塊連接起來。應當指出，信號只能沿箭頭方向通過。這樣，控制系統的方塊圖就清楚地表示了它的單向特性。

T為慣性環節的時間常數，K為比例系數。
當輸入信號為單位階躍函數時，其環節的輸出為

圖2-4表示了一個方塊圖單元。指向方塊的箭頭表示輸入，而從方塊出來的箭頭則表示輸出。在這些箭頭上標明了相應的信號。

應當指出，方塊輸出信號等于輸入信號與方塊中傳遞函數的乘積。

用方塊圖表示系統的優點是：只要依據信號的流向，將各元件的方塊連結起來，就能夠容易地組成整個系統的方塊圖，通過方塊圖，還可以評價每一個元件對系統性能的影響。

總之，方塊圖比物理系統本身更容易體現系統的函數功能。方塊圖包含了與系統動態特性有關的信息，但它不包括與系統物理結構有關的信息。因此，許多完全不同和根本無關的系統，可以用同一個方塊圖來表示。

應當指出，在方塊圖中沒有明顯表示出系統的主能源，而且對于一定的系統來說，方塊圖也不是唯一的。由于分析角度的不同，對于同一個系統，可以畫出許多不同的方塊圖。

誤差檢測器 誤差檢測器產生的輸出信號，等于控制系統的參考輸入信號與反饋信號之差。在設計中，選擇誤差檢測器是一件很重要的工作，需要仔細確定。因為誤差檢測器中的任何缺陷，都必然會降低整個系統的性能。圖2-5表示了誤差檢測器的方塊圖。

需要注意的是，圖中進行相加或相減的一些量，應具有相同的量綱和單位。

閉環系統方塊圖 在圖2-6上，表示了一個閉環系統的方塊圖。輸出量C(s)反饋到相加點，并且在相加點與參考輸入量R(s)進行比較。系統的閉環性質，在圖上清楚地表示了出來。在這種情況下，方塊的輸出量C(s)，等于方塊的輸入量E(s)乘以傳遞函數G(s)。

任何線性控制系統，都可以用由方塊、相加點和分支點組成的方塊圖來表示。所謂分支點，就是由方塊出來的輸出信號，從這一點起同時進入另一個方塊或相加點。

當輸出量反饋到相加點與輸入量進行比較時，必須將輸出信號轉變為與輸入信號相同的形式。例如，在溫度控制系統中，輸出信號通常為被控溫度。具有溫度量綱的輸出信號，在與輸入信號進行比較之前，必須轉變為力或位置。這種轉換由反饋元件來完成，反饋元件的另一個重要作用，是在輸出量與輸入量進行比較之前，改變輸出量。對于正在討論的例子，反饋到相加點與輸入量進行比較的反饋信號為B(s)=H(s)C(s)。

反饋信號B(s)與作用誤差信號E(s)之比，叫做開環傳遞函數。即

輸出量C(s)與作用誤差信號E(s)之比，叫做前向傳遞函數，因而

如果反饋傳遞函數等于1，那么開環傳遞函數與前向傳遞函數相同。在圖2-6所示系統中，輸出量C(s)與輸入量R(s)的關系，可推導如下：

C(s)=G(s)E(s)
E(s)=R(s)-B(s)=R(s)-H(s)C(s)

從上述方程中消去E(s)，得

C(s)=G(s)[R(s)-H(s)C(s)]

于是可得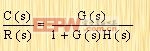

(2-17)

C(s)與R(s)之間的傳遞函數，叫做閉環傳遞函數。這一傳遞函數，將閉環系統的動特性，與前向通道元件和反饋通道元件的動態特性聯系在一起了。

由方程（2-17），可求得C(s)為

因此，閉環系統的輸出量，顯然取決于閉環傳遞函數和輸入量的性質。

擾動作用下的閉環系統 圖2-7為一個在擾動作用下的閉環系統。當兩個輸入量（參考輸入量和擾動量）同時作用于線性系統時，可以對每一個輸入量單獨地進行處理，將與每一個輸入量單獨作用時相應的輸出量疊加，即可得到系統的總輸出量。每個輸入量加進系統的形式，用相加點上的加號或減號來表示。

現在來討論圖2-7上表示的系統。在研究擾動量N(s)對系統的影響時，可以假設系統在開始時是靜止的，并且假設無誤差信號，這樣就可以單獨計算系統對擾動的響應CN(s)。這一響應可由下式求得：

另一方面，在研究系統對參考輸入量的響應時，可以假設擾動量等于零。這時系統對參考輸入量R(s)的響應CR(s)可由下式求得：

將上述兩個單獨的響應相加，就可以得到參考輸入量和擾動量同時作用時的響應。換句話說，參考輸入量R(s)和擾動量N(s)同時作用于系統時，系統的響應C(s)為

另一方面，當G1(s)G2(s)H(s)的增益增大時，閉環傳遞函數CR(s)/R(s)趨近于1/H(s)。這表明，當 >>1時，閉環傳遞函數CR(s)/R(s)將變成與G1(s)和G2(s)無關，而只與H(s)成反比關系，因此G1(s)和G2(s)的變化，不影響閉環傳遞函數CR(s)/R(s)。這是閉環系統的另一個優點。可以容易地看出：任何閉環系統，當反饋傳遞函數H(s)=1時，系統的輸入量與輸出量相等。

畫方塊圖的步驟 在繪制系統的方塊圖時，首先列寫描述每一個元件動態特性的方程式。然后假定初始條件等于零，對這些方程式進行拉普拉斯變換，并將每一個拉普拉斯變換方程分別以方塊的形式表示出來。最后將這些方塊單元結合在一起，以組成完整的方塊圖。

方塊圖的簡化 應當強調指出，只有當一個方塊的輸出量不受其后的方塊影響時，才能夠將它們串聯連接。如果在這些元件之間存在著負載效應，就必需將這些元件歸并為一個單一的方塊。
任意數量串聯的、表示無負載效應元件的方塊，可以用一個單一的方塊代替，它的傳遞函數，就等于各單獨傳遞函數的乘積。

一個包含著許多反饋回路的復雜的方塊圖，可以應用方塊圖的代數法則，經過逐步重新排列和整理而得到簡化。在表2-1中，列舉了一些比較常見的方塊圖代數法則。這些代數法則說明，同一個方程式可以用不同的方法表示。通過重新排列和代換，將方塊圖簡化后，可以使以后的數學分析工作很容易進行。但是應當指出，當方塊圖得到簡化后，新的方塊卻變得更加復雜了，因為產生了新的極點和零點。

3
4

在方塊圖簡化過程中，應記住以下兩條原則：

1．前向通道中傳遞函數的乘積必須保持不變；
2．回路中傳遞函數的乘積必須保持不變。

方塊圖簡化的一般法則是移動分支點和相加點，交換相加點，減少內反饋回路。下面舉例說明方塊圖的變換和化簡。