基于優化GDTW-SVM算法的聯機手寫識別
3 優化GDTW-SVM算法
盡管GDTW-SVM獲得了較高的識別率,但是其計算復雜度高。DTW算法的計算復雜度是O(NT,NR),而SVM算法在訓練和識別過程中需要反復使用GDTW核函數,對于嵌入式設備的計算能力要求較高。因此,需要對GDTW核函數進行優化。
分析圖1中的最優對齊路徑,當兩個樣本完全相同時,最優對齊路徑和對角線重合;當兩個樣本有所差別時,最優對齊路徑偏離對角線,且差別(DTW距離)越大最優路徑越偏離對角線。下面以字母m和n為例,進一步分析以上結論。
(1)依次從字母n的所有訓練樣本中選擇一個樣本,計算其到字母n的所有訓練樣本最優對齊路徑,并規整到80’80矩陣;
(2)將所有計算結果疊加后得到n-n最優對齊路徑疊加圖;
(3)繪制疊加圖,即圖2的第一幅圖,圖中像素點灰度越高,代表越多最優對齊路徑經過此點。同理,繪制n-m最優對齊路徑疊加圖和m-m最優對齊路徑疊加圖,分別為圖2的第二和第三幅圖所示。本文引用地址:http://www.104case.com/article/193871.htm

從圖2可以看到,兩個相同或相似字符的最優對齊路徑集中在對角區域:由于n的不同樣本、m的不同樣本的起筆寫法比收筆寫法隨意,第一和第三幅圖的對角區域的左下角比較寬;n和m的最優對齊路徑在對角區域中分布較均勻,且第二幅圖顯示對角區域的中部有明顯的低灰度區域。
假設訓練樣本可以代表聯機手寫字符的特征,則可以通過僅計算對角區域中的最優對齊路徑來優化GDTW核函數。計算兩個樣本T=(t1,…,tNT)和R=(r1,…,rNR)的GDTW核函數時,假定二者屬于相同的字符類,那么二者的差別不大,因此,在GDTW核函數計算中引入參數k和τ

式(9)中lbottom,ltop,lleft,lright如圖3所示。引入參數k和τ之后,不在NT×NR的矩陣中求解式(8),而是在k和τ約束的區域(即圖3中兩條虛線所夾的對角區域)中求解,計算最優對齊路徑。
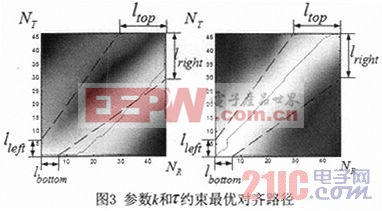
從直觀的角度看,參數k和τ減少了最優對齊路徑的計算空間,因此,修改后的GDTW核函數的計算時間減少。而另外一方面,如果參數τ保持不變(如τ=0.6),參數k越小,最優對齊路徑的前端的計算被約束在越小的空間,迫使其“最優”對齊路徑的計算選擇非最優對齊路徑,即參數k是兩個字符樣本頭部的相識程度的權重;類似地,參數τ是兩個字符樣本尾部的相識程度的權重。參數k和τ的權重作用對于如數字“0”和“6”等相似字符的分類有重要意義。




評論