如何在低算力MCU平臺上優雅的計算均值和方差

一維數據的均值和方差計算可以說是幾乎是最常用的統計分析方法。這個初中就學過的概念，在嵌入式系統中卻有著廣泛的實際應用：

■ 傳感器故障檢測

□ 正常工作的傳感器數據波動應在一定范圍內

□ 突然的均值漂移或方差劇變，往往意味著傳感器故障

□ 如溫度傳感器讀數突然劇烈波動，很可能是接觸不良 

信號質量評估 

□ GPS信號強度的均值和方差可以反映定位質量 

□ 方差過大說明信號不穩定，可能處于多路徑效應區域

□ 均值過低說明信號較弱，可能在遮擋環境下

■ 機器人控制

□ 舵機位置反饋的方差可以用來檢測是否卡死

□ 電機電流的均值可以估計負載大小

□ 輪速反饋的方差可以判斷地面情況

■ 電池管理

□ 電壓的滑動均值可以平滑瞬時波動

□ 電流的方差可以反映負載的穩定性

□ 溫度的異常波動可能預示電池問題

這些場景都需要實時、高效地計算數據流的統計特征。雖然計算公式簡單，但在實際工程中，有限的資源限制及實時性要求、數值穩定性和存儲效率成為主要挑戰。

本文主要探討如何在有限的計算能力和內存條件下，優雅地實現高效的均值和方差計算。通過優化算法、減少計算復雜度、利用遞推公式和定點數運算，文章提供了一系列使用技巧，幫忙開發者在保持精度的同時，顯著降低計算開銷。這些方法特別適用于物聯網設備、嵌入式系統等對資源敏感的領域。

基礎知識

1.1 定義 

眾所周知: 均值(mean)反映數據的集中趨勢：

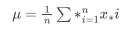
方差(variance)反映數據的離散程度：

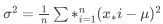
基于以上兩個定義式出發,可以很簡單的轉換為C code, 淺顯易懂: 

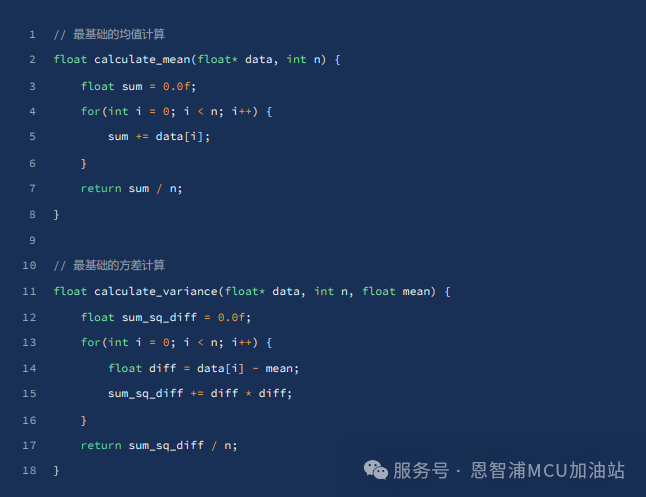
使用示例：

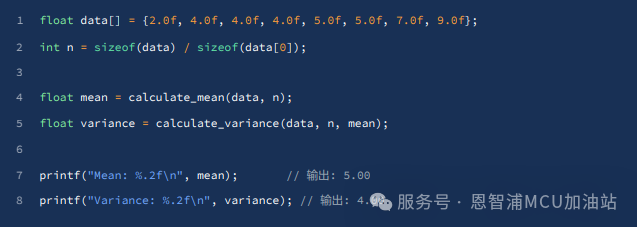
但是這種最基礎的實現存在幾個嚴重問題: 

1） 數據存儲問題 

● 需要保存全部歷史數據

● 對于高頻采樣的傳感器（如IMU 200Hz），1s就需要存儲200個數據點

● 在嵌入式系統中，內存資源寶貴，這種方式極其浪費

2）計算效率問題 

● 每次計算都需要遍歷全部數據，時間復雜度為O(n)

● 對于實時系統，隨著數據量增加，計算延遲會越來越大

● 不適合需要快速響應的實時控制系統

3）數值穩定性問題 

● 直接累加可能導致數值溢出

● 對于很大或很小的數據，浮點數精度損失明顯

● 特別是在計算方差時，（Xi-u）的計算可能產生很大的舍入誤差

4）實時性問題

● 無法進行增量計算

● 新數據到來時需要重新計算所有統計量

● 不適合流數據處理

在線算法(Online Algorithm)

在線方法也叫做流式方法, 針對批量方法的缺點,在線方法不需要保存歷史數據，在線算法中比較經典的是 Welford算法。

Welford算法是由B.P. Welford在1962年提出的一種在線計算均值和方差的算法。它的核心思想是：每來一個新數據，就遞增地更新均值和方差，而不需要存儲所有歷史數據。

2.1 Welford算法 

這是一種數值穩定的在線算法，特別適合處理數據流。Welford算法的核心是遞推公式的推導。設第n個數據到來時：

1) 均值更新

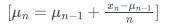
2) 方差更新：

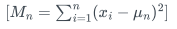
3) 關鍵推導步驟：

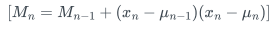
2.2 Welford算法實現2.2.1 核心結構和函數 

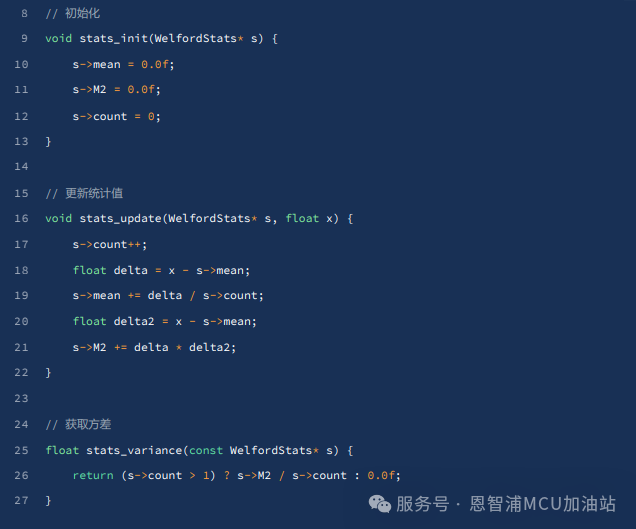
 2.2.2 使用示例 

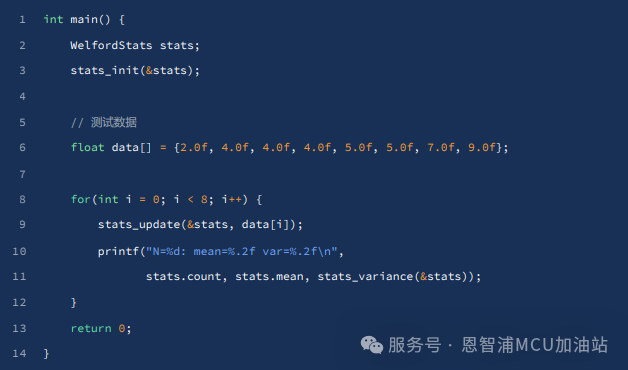
 2.2.3 算法步驟解釋

1) 每次新數據到來：

● 計數加1

● 計算新數據與當前均值的差

● 更新均值

● 更新M2（用于方差計算）

2) 方差計算：

● 直接用M2除以樣本數

● 樣本數小于2時返回0

算法對比小結

本文介紹了Welford方差計算方法，它是一種在線、一次遍歷的方差計算算法，能在不存儲所有樣本的情況下，逐步計算所有樣本的方差。與傳統的方差計算方法相比，Welford方法在降低訪存次數的同時，也做到了數值計算的穩定性。因此，Welford方法更適合處理海量數據，也更適合在高性能計算環境中使用。

事實上，Welford算法啟發了 NVIDIA 在2018年提出的Online Softmax算法，該算法降低了Softmax計算的訪存次數，提高了計算性能。而Online Softmax則直接啟發了FlashAttention，后者已經成為支撐當前最流行的Transformer架構的最核心的計算優化手段。