基于優化GDTW-SVM算法的聯機手寫識別
加入技術交流群
2 GDTW-SVM算法
2．1 支持向量機
假設線性分類器對輸入的特征向量x={x1，x2，…xn}(n是樣本數目)，輸出Y={y1，y2，…，yn}其中，xi，I RN，N是特征向量的維數：yi∈{-1，1}， yi=-1表示樣本(xi，yi)屬于第一類，yi=1表示樣本(xi，yi)屬于另一類。該線性分類器的分類決策為
y(w·x>+b)≥1 (2)
式(2)中(w,b)確定分類超平面w·x>+b=0。
SVM以最小化結構風險為目標，計算使得訓練樣本集到分類超平面的距離最大化的最優分類超平面。其等價于對式(2)求解凸二次規劃問題。
式(4)中ai是拉格朗日乘子，靠近超平面的點對應的ai非零，其它所有點對應的ai為零。因此，最優分類決策的對偶表示
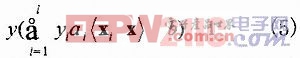
只包含ai非零的點。這些點稱為支持向量(Support Vector，SV)，支持向量決定了最優分類超平面，且其數目越多，分類判決的計算時間越長。
對于非線性可分樣本，SVM使用滿足Mercer定理的核函數K(x，z)，代替式(5)中的內積計算，將輸入的特征向量映射到高維線性可分的特征空間。Merce定理保證了核函數的正定對稱性和式(4)最優化問題求解過程的收斂性。一個比較常用的核函數是高斯核函數(GRBF)
KGRBF(X，Z)=exp(-y·‖X-Z‖p)，p=1，2，… (6)
2．2 GDTW核函數
假設T=(t1，…，tNT)和R=(r1，…，rNR)
是長度分別為NT和NR的特征向量序列。對齊路徑f=(f(1)，…，f(L))是對齊序列T和R的索引序列，其中，L是路徑長度，
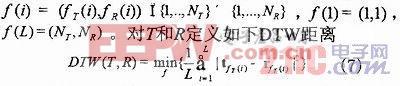
即尋找使平均距離最小的最優對齊路徑。DTW距離越小，T和R所代表的樣本越相似。可以使用動態規劃(Dynamic Programming)算法計算最優對齊路徑和DTW距離。
圖1給出了最優對齊路徑和DTW距離的示例，其中，上半部分是字符樣本的繪圖，順次是“oocae”；下半部分是各個字符樣本與第一個字符樣本的最優對齊路徑和DTW距離。本文引用地址：http://www.104case.com/article/193871.htm
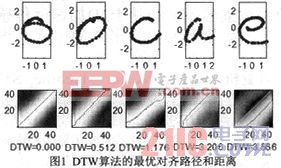
Bahlmann等人使用DTW距離代替高斯核函數(6)中的歐幾里德距離‖X-Z‖p的計算(取p=2)，構造了GDTW核函數
KGRBF(X，Z)=exp(-y·DTW(X，Z)) (8)
他們的聯機手寫識別實驗的結果和Bothe等人的實驗結果表明，GDTW-SVM取得了比GDTW-SVM和k近鄰算法(k-Nearest Neighbor，kNN)更高的識別率，而且在不同聯機手寫識別數據庫子集的識別實驗中，與基于其它彈性距離計算的核函數的SVM相比，各有優劣且識別率的差值在0．3％以內。
評論