基于DMFT的LFM信號參數估計

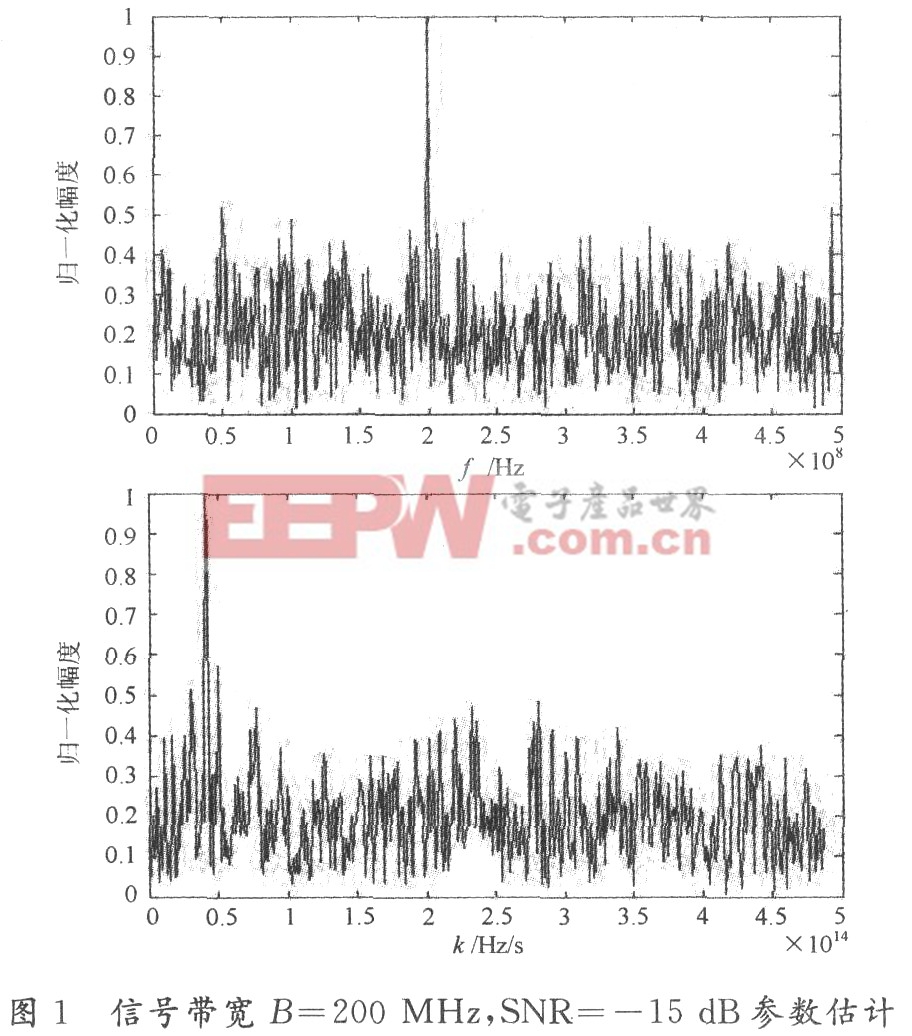
表l為B=200 MHz時不同信噪比情況下初始頻率和調頻斜率的測量值與其對應真值(f0=200 MHz，k0=4．0×1012Hz／s)的絕對誤差。

從以上結果可以看出，該方法對信號參數的估計有較高的精度，在SNR=一15 dB的情況下還能估計信號參數，這是一般的時頻分析方法不能比擬的。SNR低于一15 dB時，參數估計絕對誤差將逐步增大，信號經過離散匹配傅里葉變換淹沒在隨機噪聲中，無法正確檢測信號。
4．2 多分量LFM信號仿真
離散匹配傅里葉變換是一種線性變換，所以在對多分量信號進行分析時不會產生交叉項。但是信號中強分量LFM信號的旁瓣可能大于弱信號的主瓣峰值，影響到多分量LFM信號的分辨和參數估計。為了解決這個問題，借助“Clean”的思想：首先計算多分量LFM信號的離散二步匹配傅里葉變換，然后進行二維搜索找極大值。并根據峰值的位置和大小估計最強LFM信號分量的幅度、初始頻率和調制斜率，然后由上述參數重構LFM信號并從信號之減去，最后將處理過的信號重復上述過程估計下一個LFM信號的參數。
多信號的參數估計仿真采用如下信號：

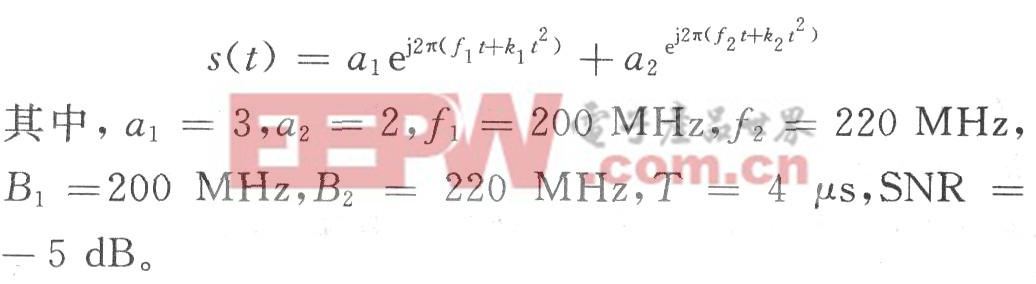
進行第一次DMFT之后信號頻譜如圖2所示，只出現強信號分量的一個峰值，弱信號的峰值淹沒在強信號分量的旁瓣中。此時，在圖2中搜索譜峰最大值，得出強信號的分量：f1=2.002x108，k1=4.96x10 13，一個分量s1(t)，得到剩余信號s2(t)，再進行一次二步DMFT，對其余LFM信號分量估計，得到如圖3所示結果，估計得到第二個分量的參數：f2=2．197×108，k2=5．53×1013，a2=1．89。

上面的仿真結果表明，離散匹配傅里葉變換結合“clean思想是一種檢測多分量LFM信號的有效的方法。仿真進一步表明，當較小分量的信噪比不小于一15 dB時，LFM信號的參數估計能達到較高的精度。隨著信噪比的進一步降低，參數估計精度將下降，無法正確估計信號的參數。

5 結 語
首先介紹了LFM信號的形式以及DMFT的基本原理，然后從減小運算量的角度對DMFT算法進行改進，最后分別對單分量和多分量LFM信號進行Matlab仿真，結果表明，DMFT能夠在低SNR情況下估計出LFM信號的參數，不存在多分量信號交叉項問題，而且運用本文改進的算法運算量較小，在對低截獲概率雷達信號的處理中將有廣闊的應用前景。