基于VerilogHDL的小波濾波器的設計與實現

0 引 言
現代計算機和通信系統中廣泛采用數字信號處理的技術和方法，其基本思路是先把信號用一系列的數字來表示，然后對這些數字信號進行各種快速的數學運算。其目的是多種多樣的，有的是為了加密，有的是為了去掉噪聲等無關的信息，稱為濾波；有時也把某些種類的數字信號處理運算成為變換，如離散的傅里葉變換(DFT)，小波變換(Wavelet T)等。VerilogHDL是目前應用最廣泛的一種硬件描述語言，用于數字電子系統的設計。可用它進行各種級別的邏輯設計，并進行數字邏輯系統的仿真驗證，時序分析，邏輯綜合。小波濾波器的設計屬于復雜算法的電路設計，因此利用Veril―ogHDL對雙正交小波濾波器進行建模、仿真，實現電路的自動化設計，將是一種較為理想的方法。

l 小波濾波器的設計
對于小波函數，要求它具有正交性、緊支集、對稱性和平滑性。正交性可以使變換無冗余；緊支集則帶來優良的空間分辨率；對稱性保證了與其對應濾波器的相位為線性；平滑性可以產生較小的失真。這樣使離散二進小波變換受到很大的限制，為此，人們提出一種雙正交的小波變換。本文設計小波濾波器正是基于雙正交小波變換的一種雙通道完全重構濾波器，因此可以對信號進行分解后實現精確重構，所以對信號的濾波有很好的作用。由于它具有正變換二元上抽樣采樣和反變換二元下抽樣采樣特性，在進行濾波器設計時可以將雙正交小波濾波器設計成具有多相結構的雙通道完全重構濾波器。雙正交小波變換可以看成原始信號通過一系列高低通濾波器濾波并經過抽樣后所得到的結果，重構過程與此相反。為了使變換后的信號能夠完全重建，須滿足Y(n)=x-kX(n)，在這里取k=1。雙正交小波濾波器分解和重構過程如圖1所示。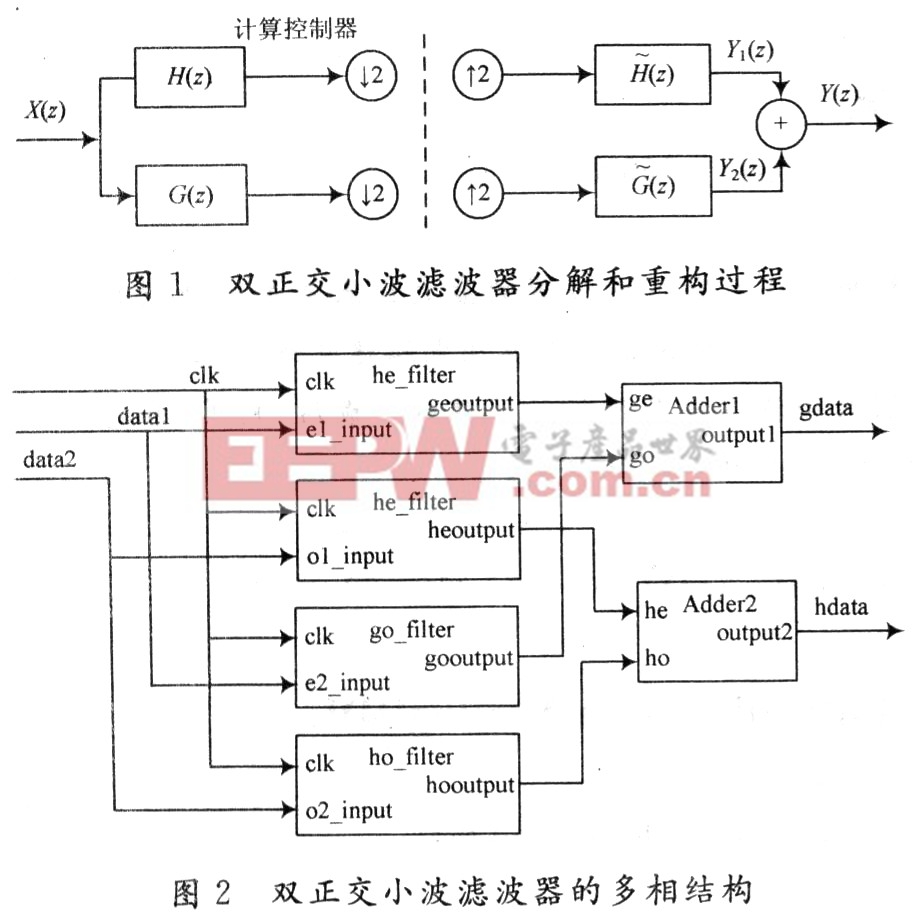

設G(z)，H(z)分別為分解低通，高通濾波器，下采樣后用H(z)濾波等價于先用H(z2)濾波，然后下采樣，所以：

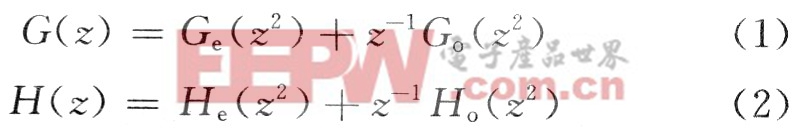
其中：Ge和Go分別是G(z)的偶數項和奇數項，He和H。分別是H(z)的偶數項和奇數項。根據式(1)，式(2)可以建立雙正交小波濾波器的多相結構模型如圖2所示。
下面對雙正交小波濾波器用VerilogHDL進行頂層設計：