仿真擴展芯片簡化高速汽車嵌入式處理器的集成

3 仿真實驗

　　一個典型的工業過程的傳遞函數為

　　期望跟蹤輸入信號為周期T1 =4s，振幅A1 =±2 的方波信號。圖2 和圖3 分別為MRAS 在期望跟蹤輸入信號作用下的輸出跟蹤曲線和誤差曲線。仿真結果表明，“抖動”現象已被消除，系統的跟蹤性能和收斂性都已得到大大的改善和提高。

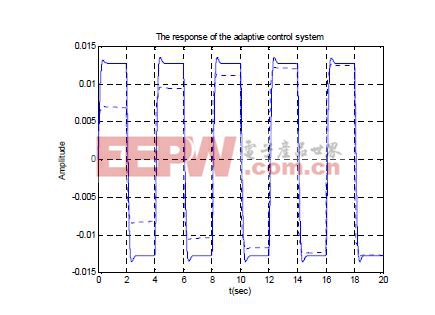
圖2 方波輸入信號和MRAS 在該信號作用下的跟蹤曲線

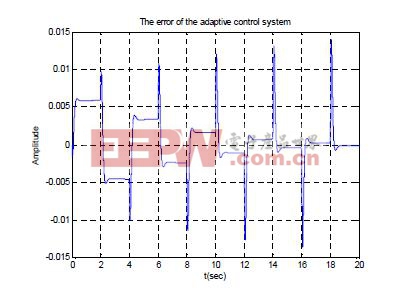
圖3 MRAS 在方波輸入信號作用下的誤差曲線

　　4 結束語

　　用傳統控制方法對具有時變參數的線性系統進行控制和分析存在較大的困難。本文在對這類系統的分析的基礎上，提出了一種利用Lyapunov 穩定性理論設計MARS 的控制策略。此控制律直接以系統的狀態變量為基礎，對被控對象施行(K,F) 變換以構成自適應控制律。仿真結果表明了該控制策略不僅克服了一般自適應控制存在的“抖動”現象，而且在跟蹤性能和收斂性方面都具有較好的改善，在一類具有參數時變實際工業過程的控制問題方面具有重要的應用價值。

　　參考文獻

[1] Tsakalis K S,Ioannou P A.Adaptive control of linear time-varying plants.Automatica,1987,23:459~468
[2] Middleton R H,Goodwin G C.Adaptive control of time-varying linear systems.IEEE Trans.Autom.Control,1988,33(2):150~155
[3] Tsakalis K S,Ioannou P A.Linear Time-varying Systems Control and Adaption.New Jersey:Prentice Hall,1993
[4] 李眉眉,劉玉生,余義.基于MATLAB 的時變系統自適應控制的仿真. 微計算機信息[J], 2004,8:31~32
[5] 殷斌,馮純伯.線性離散時變系統的魯棒自適應控制.自動化學報[J],1999,25:786~790
[6] 王春曉, 李俊民. 不確定關聯大系統對時變參數的自適應控制. 控制與決策[J],2004,6:687~690

　　本文作者創新點：文章針對一類典型的參數時變的實際工業過程，基于模型參考自適應控制（MRAC）理論，提出了一種新的自適應控制方案。仿真結果表明該控制方案能夠消除傳統控制算法中的“抖動”現象，系統的跟蹤性能和收斂性也得到較大的改善和提高。