仿真擴展芯片簡化高速汽車嵌入式處理器的集成

　　1 引言

　　由于缺乏適當的數學手段以及自適應系統本身嚴重的非線性，對具有時變參數的線性系統進行控制分析是非常困難的。應該指出，時變系統自適應控制的關鍵在于，如何提高系統對由參數時變引起的攝動的魯棒性能。傳統的時變系統的自適應控制，大多是用魯棒自適應律來進行時變參數的估計，從而保證閉環系統的穩定[1~3] 。另外，為了克服采用局部參數最優化方法設計出的MRAS(model reference adaptive system，模型參考自適應系統)不一定穩定的缺點，德國學者Parks 于1966 年提出了采用Lyapunov （李雅普諾夫）第二法推導MRAS 的自適應控制律，以保證系統具有全局漸近穩定性。

　　本文在自適應思想的基礎上，利用李雅普諾夫穩定性理論設計MRAS，并利用系統的狀態變量構成自適應控制律，提高自適應算法對于帶有包括未知時變參數等不確定對象的魯棒性能。該方法的另一個特點是消除了傳統控制算法中的“抖動”現象，改善了系統的性能。作者把這種思想用于一類典型的線性連續時變系統的自適應跟蹤控制，仿真結果證實了算法的可行性。

　　2 問題描述

　　模型參考自適應控制（MRAC）是一種重要的控制設計方法，這里主要采用Lyapunov 穩定性理論設計自適應控制器，并假設可以獲取對象的狀態變量，因此可以直接利用這些狀態變量構成自適應控制律[4] 。

　　2.1 對被控對象施行(K,F)變換的MRAS 設計方法

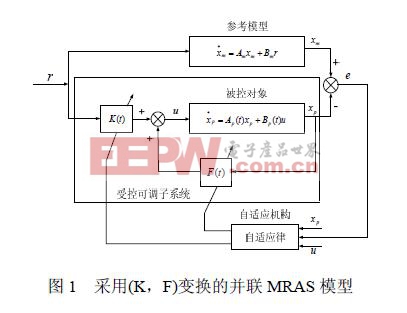
圖1 采用(K，F)變換的并聯MRAS 模型

　　若MRAS 采用圖1 所示的并聯結構，設被控對象的狀態方程為

　　由式(1)、(2)和(3)得

　　Q 為選定的正定矩陣。

　　為了使閉環系統在Lyapunov 意義下穩定，應該V0 。通過求解可以得到K(t) 和F(t) 的更新律：　

　　可以近似用K 代替。

　　2.2 控制器的穩定性分析定理.