正交幅度調制解調器的FPGA設計與仿真
加入技術交流群
2 正交信號發(fā)生器的設計
2．1 CORDIC算法原理
CORDIC算法是由J．Volder于1959年提出的。該算法適用于解決一些三角學的問題，如平面坐標的旋轉和直角坐標到極坐標的轉換等。 CORDIC算法的基本思想是通過一系列固定的、與運算基數有關的角度的不斷偏擺，以逼近所需的旋轉角度。從廣義上講，CORDIC方法就是一種數值計算的逼近方法。該算法實現三角函數的基本原理如下：
設初始向量(x0，y0)逆時針旋轉角度口后得到向量(xn，yn)，則：
式中：θi表示第i次旋轉的角度，并且tanθi=2-i；zi表示第i次旋轉后與目標角度的差；δi表示向量的旋轉方向由zi的符號位來決定，即δi=sign(zi)；
為每一級的校正因子，也就是每一級旋轉時向量模長發(fā)生的變化，對于字長一定的運算，總的校正因子是一個常數。迭代n次(n→∞)后可以得到如下結果：
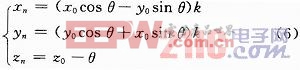
當給定的初始輸入數據為x0=1／k，y0=0時，z0=θ，則輸出為：
由上可知，xn，yn分別為輸入角θ的余弦和正弦值，故基于CORDIC算法可產生正交信號。
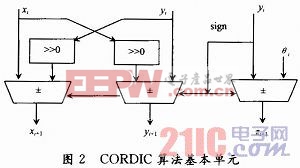
2．2 CORDIC算法流水線結構
由式(5)可以看出，CORDIC算法的實現只需要基本的加減法和移位操作，因此很容易用硬件實現。該硬件的實現可以通過圖2所示的基本單元級聯(lián)成流水線結構實現。在經過n(迭代次數)個時鐘的建立時間之后，每隔一個時鐘便能輸出一個運算結果。輸出精度由CORDIC算法中的迭代次數決定。如需提高精度，只需簡單地增加流水單元即可，擴展性很好，而且這并不會大量增加FPGA的資源耗費。本文引用地址：http://www.104case.com/article/190890.htm
評論