基于FPGA的多項式運算器設計
3 運算器設計
3.1 四則運算電路
文獻中瞄述了各種無符號整數間的運算電路。雖然也可以進行用反碼表示的符號數的運算,但不傾向于使用。因為需要做四則混合運算;反碼易于做加、減法,但不易做乘、除法。而用非反碼的帶符號位的數據,符號位做單獨計算,其余數據做無符號運算,整個計算結構是最簡單的。另外即便是無符號數做除法也很復雜,不過考慮到有種特殊的除法運算除外,那就是對于二進制數去掉最末位就相當于除以2。所以運算時可以盡量避免除以非2倍數的數,以此來簡化計算。
表示小數在計算中是必須的。文獻中介紹了二進制定點小數,比如需要保留數的2位二進制小數位,可以將二進制小數“…b3b2b1.a1 a2”表示為:
運算中還是可以視為對整數的計算。這樣用無符號的定點數進行計算,配合獨立的符號位表示正負,就可以用簡單的無符號運算器進行復雜的運算。
3.2 多項式的變換
式(4)為一個3次多項式,以它為例來介紹設計方法:
y=a0+a1×x+a2×x2+a3×x3 (4)
首先將式(4)中所有的數都用一個符號位加無符號二進制形式表示。分別用N1,N2表示y和x中包含的小數位數,可以將式(4)寫成:
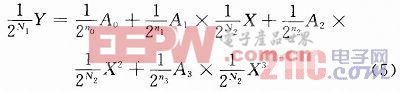
式中:X,Y是x,y去掉小數點后的整數(注:這里和式(3)一樣只是去掉小數點,不是去掉小數位)。A0,A1,A2,A3作為系統的常數也是一樣;n0,n1,n2,n3分別是a0,a1,a2,a3二進制形式的小數位數。可以進一步變換式(5)為:
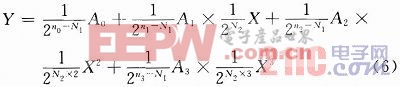
不難發現式(6)是很容易實現的。先進行各項符號位的計算,然后就只剩下無符號整形數據計算;而且除法全是除以2的倍數。最后各項之間根據符號位做加、減運算就得到輸出Y,是帶符號有N1位小數的定點數。













評論