基于FPGA的FFT算法優化及其在磁共振譜儀中的應用

如果用一般的定點計算，信噪比下降，噪聲會將產生的鏡像峰湮滅，因此必須采取一定的措施減小由定點化產生的誤差。考慮到在64點FFT并行模塊里點數是固定的，進行蝶形運算時旋轉因子是常數，因此可以根據系數的特點對定點化時的階碼做動態調整，在保證無溢出的條件下最大程度的減小噪聲。

如圖5所示，對比在Matlab中的仿真結果，在沒有采取動態調整措施前進行定點化的噪聲量級達到±1(見圖5(a))，進行動態調整后下降到10-3(見圖5(b))，可見采用動態調整進行定點化可以有效地降低由于有限字長效應引起的噪聲。

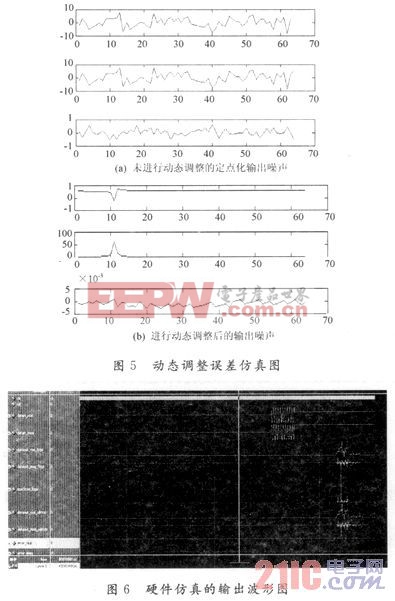
圖6為進行動態調整后在FPGA硬件運行的仿真結果，與軟件自帶的FFT IP相比誤差很小，在輸入正弦波的時候可以明顯地觀察到尖峰，這樣的結果足以滿足NMR譜儀的信號檢測要求。

2．2 64點FFT并行模塊資源優化

由于64點FFT模塊并行實現，所占用的FPGA邏輯資源太多，在一般的FPGA中難以實現，因此有必要對其進行優化減少所占用的資源。該設計中N是確定的，旋轉因子都是常數，蝶形運算中的復數乘法為常系數乘法，根據這個特點，可對使用資源進行優化。

如式(9)所示，64點FFT可分解為384個蝶形運算單元。

n=Nlog N (9)

式中：N為FFT點數；n為所需的蝶形運算單元的個數。

式(5)和(6)各包含1個復數加法運算和1個復數乘法運算，需要2個加法器和4個乘法器實現。但經過如式(10)所示的運算后的復數乘法可用三乘法器實現，因此綜合后的資源先比四乘法器架構優化了25％，

(A1+B1i)(A2+B2i)=(A1A2-B1B2)(A1B2-A2B1)i=A1(A2+B2)=B2(A1+B1)+[A1(A2+B2)-A2(A1+B1)] (10)