采用歐氏算法和頻譜結構分析相結合的RS硬件解碼方

差錯控制編碼技術對改善誤碼率、提高通信的可靠性具重要作用。RS碼既可以糾正隨機錯誤，又可以糾正突發錯誤，具有很強的糾錯能力，在通信系統中應用廣泛。由于RS碼的譯碼復雜度高，數字運算量大，常見的硬件及軟件譯碼方案大多不能滿足高速率的傳輸需求，一般適用于10Mbps以下。本文提出的歐氏算法和頻譜結構分析相結合的RS硬件解碼方案，適用于FPGA單片實現，速率高、延遲小、通用性強、使用靈活。筆者在FPGA芯片上實現了GF（2 8）上符號速率為50Mbps的流式解碼方案，最大延時為640ns，參數可以根據需要靈活設置。

　　1 RS碼的結構

　　碼字長度為N=q-1(q=2i)，生成多項式為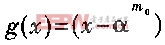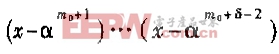，αi∈GF(q) 的RS碼有最小碼距δ=2t+1，能夠糾正t個隨機或突發錯誤[1]。本文列舉的方案測試中采用的RS碼主要參數為N=255、m0=0、t=8，其中 GF（2 8）的生成多項式為g（x）=x8+x4+x3+x2+1。由于RS碼的編碼邏輯結構比較簡單，文中僅給出仿真結果。

　　2 RS碼的譯碼算法

　　RS譯碼算法一般分為三步：伴隨式計算、關鍵方程獲得和錯誤圖樣的求解。其中關鍵方程的獲得是RS譯碼中最困難、最為關鍵的一步。

　　在利用伴隨式求解關鍵方程時，BM算法和Euclidean（歐氏）算法是兩種較好的選擇。BM算法涉及大量的變量存儲和復雜的邏輯控制，適用于軟件編程而不適合硬件實現。歐氏算法數據存儲量少、控制便捷，適合硬件實現。且采用歐氏算法確定關鍵方程所需時間與錯誤個數成正比，因此從處理時間上考慮，歐氏算法也是較好的選擇。

　　在獲得關鍵方程后，采用時域處理方法，需要大量的運算單元和控制電路，在硬件實現中是不可取的。而采用頻譜結構分析方法，利用最短線性移位寄存器綜合及離散傅氏逆變換進行處理，邏輯簡單、耗時少，適合硬件實現。雖然在傅氏變換時需要較多的邏輯單元，但對GF（2n）在n10的情況下，變換域譯碼器要比時域譯碼器簡單得多。因而本文提出歐氏算法和頻譜結構分析相結合的方案，并在實踐中獲得了較好的效果。

　　Euclidean算法[3]步驟如下：

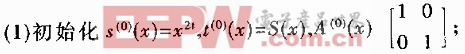
　　（2）按所列方法進行迭代

　　3 方案流程

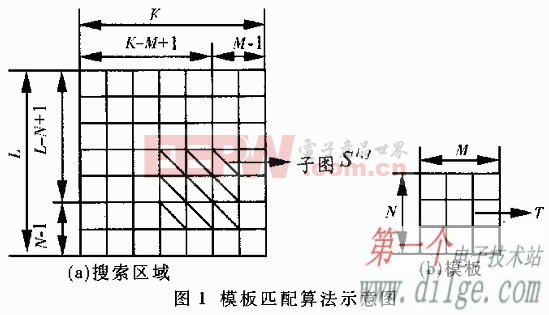
　　方案流程框圖如圖1所示。

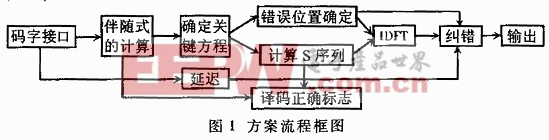
　　3.1 伴隨式S0,S1,…，S2t-1的計算

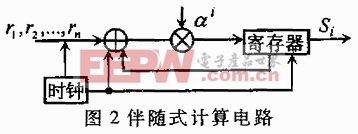
　　令r1,r2，…，rn為接收到的RS碼字，根據系統碼監督矩陣的特性，可構造如圖2所示伴隨式計算電路Si=（（（r1αi+r2）αi+r3）αi…+rn，從而實際伴隨式序列的計算。