基于SS序列集成電路不規則模塊布圖算法
在SS解碼算法中還需將模塊翻轉以獲得更好地擺放位置。由于不規則模塊被劃分成許多小矩形,翻轉時不能簡單改變矩形的長寬順序,而應結合模塊區域連接序列進行整體翻轉。不同于簡單矩形模塊只有0°和90°2種狀態,而不規則模塊要復雜得多,其中包括0°、90°、180°和270° 4種翻轉狀態,如圖3所示。本文引用地址:http://www.104case.com/article/188220.htm

3.1 180°翻轉算法
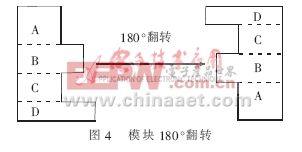
180°翻轉情況相對較為簡單,從圖3中可看出180°翻轉僅僅是在原始狀態的基礎上改變了劃分的小矩形的上下位置關系,并沒有改變這些小矩形的長寬數據,因此只需改變模塊區域連接序列中對應組的順序。設有模塊區域連接序列:XXXX0ABCD0XXX0XXX0XXX,要使矩形組ABCD組成的模塊進行180°翻轉,只需將序列改變為XXXX0DCBA0XXX0XXX0XXX即可,如圖4所示。
3.2 90°翻轉算法
90°翻轉的情況較為復雜,不僅涉及到模塊區域連接序列,而且由于其改變了小矩形的長寬數據,同時要改變模塊數據序列。首先要對模塊重新進行劃分:
(1)在原有模塊數據序列中找出長度最小的模塊,將其寬加上改組中所有模塊寬度,作為一個新的小矩形。
(2)找出原有模塊數據序列中長度第2小的模塊,將其長減去(1)中矩形的長作為其新的長度,其寬改為原來寬度加上改組中所有模塊寬度再減去(1)中長度最小的模塊的寬度。
(3)重復以上步驟直至所有矩形被處理。
(4)將修改過的模塊數據序列中長寬數據對換。
(5)修改模塊區域連接序列使其與現在的模塊數據序列相對應。
模塊90°翻轉如圖5所示。

3.3 270°翻轉算法
270°相當于在90°翻轉的基礎上再次180°翻轉,因此只需在3.2節的基礎運用3.1節的算法進行翻轉即可。
本文在SS序列算法的基礎上進行了改進,使原有算法在只能進行簡單矩形模塊布圖的基礎上,可以對一些復雜的不規則模塊進行布圖,大大增加了SS算法的實用能力和處理復雜模塊的能力,為將來集成電路布圖的靈活多變打下了基礎。本文提出了新的模塊劃分概念,并提出了模塊區域連接算法、不規則模塊翻轉算法、模塊區域連接序列等新的算法和概念。充實了SS序列算法,增加了SS序列算法的功能,大大改進了SS算法的實用性和處理復雜情況的應變能力。












評論