智能車電磁檢測及控制算法的研究

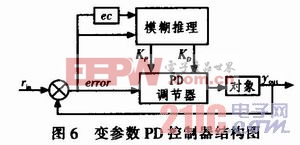
為了實現變參數PD控制，算法引入了兩個新的變量：偏移角度的變化率△α和偏移距離的變化率△d。
3．2 模糊控制規則及參數的整定
在模糊控制中取誤差α(或d)和誤差變化率△α(或△d)為輸入語言變量，以構成一個二維模糊控制器，每個語言變量取負大(NB)、負中(NM)、負小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)七個語言值。根據各模糊子集的隸屬度賦值表和各參數模糊控制模型，建立轉向模糊規則表。
參數的調整就是尋求Kp、KD與△α、△d之間的關系。智能車在運行中不斷檢測α、d和△α、△d，然后查詢模糊規則表選擇合適的Kp、KD參數進行控制。實際控制中，當△α，△d增大時，表明車體有偏離導線的趨向，這時候增加Kp、KD，阻止車體的繼續偏離；當△α，△d減小時，表明車體正逐漸趨近于導線，這時候就要減小Kp、KD。
設計中，系統首先采用基于模糊控制的變參數PD控制器分別實現單個輸入量下的控制量輸出，然后實驗得出的線性耦合關系將兩個輸出量耦合為一個量控制舵機。
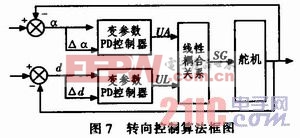
圖7所示為轉向控制算法框圖。UA為純偏移角度控制時舵機的給定量，UL為純偏離距離控制時舵機的給定量，SG為最終的舵機給定量。通過實驗得到的耦合關系為：SG=0．6UA+0．4UL。這時的舵機響應速度快，直道的跟蹤效果很好，通過彎道時可以看到比較明顯的內切。

4 速度控制算法的設計
智能車要完成起動、加速、減速、制動等動作。直線行走、拐彎和停車時要求不同的車速，因此速度必須采用閉環控制。智能車的速度與轉向是兩個獨立的被控量，但它們都是根據偏移角度α及偏離距離d來確定輸出給定量的。
根據智能車速度控制的特點，設計采用了變結構控制方法。變結構系統是指在控制過程(活瞬態過程)中，系統結構(或叫模型)可發生變化的系統。變結構控制對加給系統的攝動和干擾有良好的白適應性。對于車速的控制，當偏差較小時，采用PID控制，提高穩態精度；當偏差較大時，采用PD控制，以便加快響應速度；當偏差大于可調節范圍時，采用Bang-Bang控制。圖8所示為速度控制算法框圖。

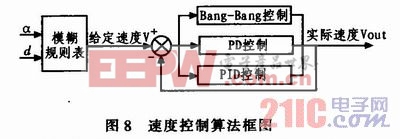
不同的偏移角α及偏離距離d通過查詢速度模糊規則表得到給定速度等級V。系統實時檢測電機的實際速度值，同當前的設定值做比較，根據誤差范圍的不同分別采用PID控制、PD控制和Bang-Bang控制。當速度誤差在±5％時采用PID控制；當速度誤差在±5％～±10％時采用PD控制；當速度誤差大于±10％時采用Bang-Bang控制。

5 結論
基于電磁傳感器的智能車的設計，可以檢測出車模相對于導線的偏移角度α及偏離距離d，并以此作為控制的輸入量。通過變參數的PD控制和變結構控制分別實現舵機和電機的精確控制。整體調試后車模速度由傳統控制方法下的1．8 m／s提高到目前的2．3 m／s，轉彎處可以看到比較明顯的內切。實驗結果表明，這種控制方法相對于單一的PID控制具有響應時間快，穩態性能好，抗干擾能力強的特點。