基于遺傳算法的復雜無源濾波器參數設計
加入技術交流群
第４步,基因操作
通常基因操作有交叉、變異、選擇三種(２)。
基因交叉：設交叉計數器ｃｃｎｔ＝０,從[０,１]范圍內產生隨機數ｒｋ（ｋ＝１,２,．．．,ＰＯＰ＿ＳＩＺＥ）,如果ｒｋ＜Ｐｃ（ｇｅｎ）,則選擇Ｘｋ為交叉用;使交叉染色體配對進行如下位交叉操作：
Ｘｊ＝[Ｘ１ｊ,Ｘ２ｊ,．．．,Ｘｐｊ,．．．,Ｘｎｊ] Ｘｊ′＝[Ｘ１ｊ,Ｘ２ｊ,．．．,Ｘｐｌ,．．．,Ｘｎｌ
Ｘｌ＝[Ｘ１ｌ,Ｘ２ｌ,．．．,Ｘｐｌ,．．．,Ｘｎｌ] Ｘｌ′＝[Ｘ１ｌ,Ｘ２ｌ,．．．,Ｘｐｊ,．．．,Ｘｎｊ]
其中Ｘｊ、Ｘｌ為配對染色體,Ｘｊ′、Ｘｌ′為交叉后染色體。
ｐ為隨機選擇的交插位,接受交叉操作的染色體個數記入ｃｃｎｔ中。基因變異：設變異計數器ｍｃｎｔ＝０,從[０,１]范圍內產生隨機數ｒｋ(ｋ＝１,２,．．．,ｎ×ＰＯＰ＿ＳＩＺＥ＋ｎ×ｃｃｎｔ),如果ｒｋ＜Ｐｍ(ｇｅｎ),則第ｋ個基因進行變異操作,并使ｍｃｎｔ＝ｍｃｎｔ＋１。新基因Ｘｋ′隨機產生于區間[(１－α)Ｘｋ,(１＋α)Ｘｋ];其中１≤ｉ≤ＰＯＰ＿ＳＩＺＥ,α為[０,１]范圍內選定常數。
染色體選擇：計算新生染色體Ｘｎ′的評價函數ｅｖａｌ(Ｘｎ′)(ｎ＝１,２,．．．,ｃｃｎｔ＋ｍｃｎｔ和父代染色體Ｘｎ的評價函數ｅｖａｌＸｎｎ＝１２．．．ＰＯＰ＿ＳＩＺＥ,并按適應性大小排列,選出其中適應性最強的ＰＯＰ＿ＳＩＺＥ個染色體構成新一代人口并保留上述過程中最佳染色體Ｖ*,這個過程稱為“適者生存”選擇。
第５步,單次過程結束判斷
當Ｆ＜Ｅｒ時(Ｅｒ為一小數量級數值,Ｘ*＝Ｖ*,輸出Ｘ*,轉第６步。
當Ｆ≤Ｅｒ且ｇｅｎ≥ＭＡＸＧＥＮ時,ｇｅｎ＝ｇｅｎ＋１,返回第３步。
當Ｆ≥Ｅｒ時且ｇｅｎ≥ＭＡＸＧＥＮ時,返回第２步。
第６步,全過程結束判斷
ｄｃｎｔ＝ｄｃｎｔ－１;當ｄｃｎｔ＞０時,返回第２步;否則,停機。
３ 數值實驗例
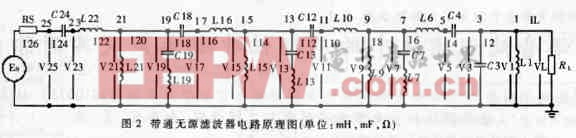
圖２為一帶通無源濾波器電路結構,通頻帶要求在９５０～１０５０ ｒａｄ／ｓ之間。為此,每隔５ ｒａｄ／ｓ作一次采樣,采樣點的幅度大于０．８５;設定低頻截止頻率為８００ ｒａｄ／ｓ,幅度小于１ｅ－５;高頻截止頻率為１３００ｒａｄ／ｓ,幅度小于１ｅ－５。建立如下優化模型：
ｓ．ｔ． ＸＬ＝[０,０,．．．,０]＜Ｘ＜ＸＵ＝[１８,１８,．．．,１８]
其中
Ｘ＝[Ｘ１,Ｘ２,．．．,Ｘ１９]＝[Ｌ,Ｃ３,Ｃ４,Ｌ６,Ｌ７,Ｃ７,Ｌ９,Ｌ１０,Ｃ１２,Ｌ１３,Ｃ１３,Ｌ１５,Ｌ１６,Ｃ１８,Ｌ１９,Ｃ１９,Ｌ２１,Ｌ２２,Ｃ２４];
Ｒ１＝１０×Ｍｉｎ(＋[１．０ｅ－５－Ｌ１]－０．０,０）,對應Ｗ１＝８００ｒａｄ／ｓ
Ｒｊ＝１．０×Ｍｉｎ(＋[Ｌｊ－０．８５]－０．０５,０);ｊ＝２,３,．．．,２２,對應Ｗｊ＝(５×ｊ＋９４０)ｒａｄ／ｓ
Ｒ２３＝１０×Ｍｉｎ(＋[１．０ｅ－５－Ｌ２３]－０．０,０）,對應Ｗ２３＝１３００ｒａｄ／ｓ
在ＮＥＣ４８００／２１０Ⅱ工作站完成上述算法。算法的參數設置為Ｅｒ＝１ｅ－６,α＝０．１,Ｐｃ＝Ｐｃ(０)＝０．６,Ｐｍ(０)＝０．１,ＰＯＰ＿ＳＩＺＥ＝４０,ＭＡＸＧＥＮ＝２０００,程序語言為ＵＮＩＸ－Ｃ。ｄｃｎｔ取１０,得到１０組設計值,皆能使頻率特性滿足要求。平均世代數為１５０８代,平均時間為９．８ｍｉｎ。其中一組結果為:
Ｘ*＝[０．０７９２１２．６５１４０．０７５２１３．０１５７０．１０５８３．３１３１
０．１７９３１３．３３８６０．０７２６０．１３３４３．３２６０．１７２２１５．１２１８０．０６３３０．０８７６１．９２８８０．３３３３１０．３１７１０．０９００]。
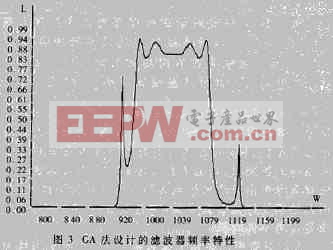
按此參數設計后,濾波器頻率特性較好地達到了預期要求,如圖３所示。
本文簡要分析了無源濾波器參數設計存在困難的主要原因。
對無源濾波器的常用電路結構,提出了計算頻率特性的簡易迭代法,并將求解滿足指標要求的參數設計值的問題轉化為優化模型的求解過程,使的原來難以描述和解決的設計問題變得明確和簡單。在遺傳算法方面,我們并不照搬前人的方法[３],例如,把最小目標函數的求解要求轉化為進化的驅動力而不是刻意求得最優解,不僅減少了計算時間,還可提供設計者多種可選擇的方案。在遺傳算法的變異階段,采用的是以現有的基因為中心的左右變異方法,有別于常用的在變量范圍內變異的方法。因本法中心不斷靈活飄移,求解過程出現兩個極端,即快速找到合適解或走入死區——永遠找不到解。我們通過設定最大世代數消除了后者的可能性,總體上提高了效率。
本法有效地克服了無源濾波器參數設計的困難,具有普遍性的價值和意義。其基本思想及原理亦可在電氣、電子、自動化等較復雜系統的參數設計領域得到廣泛的應用。本文引用地址：http://www.104case.com/article/151155.htm
評論