基于遺傳算法的復(fù)雜無源濾波器參數(shù)設(shè)計(jì)

提出了一種基于計(jì)算機(jī)數(shù)值計(jì)算的復(fù)雜無源濾波器參數(shù)設(shè)計(jì)的新方法,首先把求解電路參數(shù)的問題數(shù)學(xué)化為性能指標(biāo)優(yōu)化模型,然后采用遺傳算法求得特性符合要求的電路參數(shù)值,數(shù)值實(shí)驗(yàn)表明了此方法的有效性。

關(guān)鍵詞：無源濾波器 參數(shù)優(yōu)化設(shè)計(jì) 遺傳算法

無源濾波器在電子技術(shù)領(lǐng)域有著廣泛的應(yīng)用。針對某一應(yīng)用的復(fù)雜無源濾波器,往往結(jié)構(gòu)容易確定,參數(shù)調(diào)整卻十分困難。其原因是：結(jié)構(gòu)中的組成元件電阻、電容、電感個(gè)數(shù)較多,頻率特性與元件參數(shù)的關(guān)系是一個(gè)高階的非線性函數(shù),相互間對頻率特性的影響存在著高度的耦合,因而欲達(dá)到頻率特性優(yōu)良的設(shè)計(jì)目的,無論采用實(shí)驗(yàn)手段還是常規(guī)數(shù)學(xué)手段,都需花費(fèi)大量的時(shí)間與精力。

近年來,模擬生物進(jìn)化過程的遺傳算法作為求解優(yōu)化問題的有效手法而倍受關(guān)注。正如Ｔｈｏｍａｓ Ｂａｃｋ等人指出１,同其他手法相比,其優(yōu)點(diǎn)在于：處理問題的靈活性、適應(yīng)性、魯棒性,能取得全局解,對模型要求低,針對不同問題設(shè)計(jì)的不同遺傳算法,不僅能提高現(xiàn)有解的優(yōu)化品質(zhì),還能攻克某些難度大的優(yōu)化問題。

本文以遺傳算法的應(yīng)用為出發(fā)點(diǎn),提出了一種新的無源濾波器參數(shù)設(shè)計(jì)方法。它能有效克服上述無源濾波器參數(shù)設(shè)計(jì)的困難,十分方便地取得滿足性能指標(biāo)要求的參數(shù)設(shè)計(jì)值。

１ 優(yōu)化模型的建立

典型的無源濾波器電路組成元件一般按Ｔ型結(jié)構(gòu)連接,如圖１所示。濾波器的頻率特性可以用功率傳輸函數(shù)來定義,即：





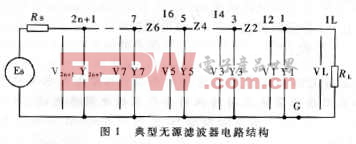
其中,Ｘ＝[Ｘ１,Ｘ２,．．．,Ｘｎ],為電路的元件參數(shù)值矩陣,ｎ為元件總個(gè)數(shù),Ｗ為頻率。若Ｘ已知,頻率采樣點(diǎn)Ｗｉ對應(yīng)的頻率特性Ｌｉ可按下述方法計(jì)算：

設(shè) Ｉ１＝ＩＬ＝０．１,

Ｖ１＝ＩＬＲＬ＋０＝ＶＬ

Ｉ２＝Ｖ１Ｙ１＋ＩＬ

Ｖ３＝Ｉ２Ｚ２＋Ｖ１

Ｖ２ｎ＋１＝Ｉ２ｎＺ２ｎ＋Ｖ２ｎ－１

Ｉ２ｎ＋２＝Ｖ２ｎ＋１Ｙ２ｎ＋１＋Ｉ２ｎ

Ｅｓ＝ＲｓＩ２ｎ＋２＋Ｖ２ｎ＋１

用簡易的迭代程序求得Ｅｓ,代入式(１)即可求得Ｌｉ。

濾波器的結(jié)構(gòu)已知后,先確定結(jié)構(gòu)中的參數(shù)取值范圍,選擇的條件可以比較寬松,然后按預(yù)期的性能指標(biāo)要求,選定適當(dāng)個(gè)頻率采樣點(diǎn)Ｗ１,Ｗ２,．．．,規(guī)定其對應(yīng)功率傳輸函數(shù)幅度界限值,迫使它調(diào)整后經(jīng)過采樣點(diǎn)時(shí),滿足幅度界限要求（大于、小于或介于）。由此獲得的新設(shè)計(jì)參數(shù)Ｘ*即是滿足預(yù)期性能指標(biāo)的設(shè)計(jì)值。為求得Ｘ*,建立如下優(yōu)化模型：



其中,Ｘ的定義同前,Ｔ＝[Ｔ１,Ｔ２,．．．]為幅度界限值矩陣,Ｓ＝[Ｓ１,Ｓ２,．．．]為加權(quán)系數(shù)矩陣,Ｕ＝[Ｕ１,Ｕ２,．．．]為裕度矩陣,ＸＬ、ＸＵ分別為設(shè)計(jì)參數(shù)的上下界限矩陣。ｐ為偶次方,ｍ為采樣點(diǎn)總數(shù),Ｒｉ稱為余差,具體表達(dá)式為：

下界 Ｒｉ＝Ｓｉ×Ｍｉｎ（＋[Ｌｉ－Ｔｉ]－Ｕｉ,０）

上界 Ｒｉ＝Ｓｉ×Ｍｉｎ（－[Ｌｉ－Ｔｉ]－Ｕｉ,０）

顯然,當(dāng)存在解Ｘ使Ｆ函數(shù)最小時(shí),Ｌｉ的值應(yīng)能控制在Ｔｉ的要求范圍內(nèi),從而使頻率特性滿足指標(biāo)要求,因此該解即可視為Ｘ*。

２ 優(yōu)化模型的求解

遺傳算法是一個(gè)強(qiáng)有力的求優(yōu)算法,它首先隨機(jī)地產(chǎn)生一組潛在的解Ｘ（該解稱為“染色體”,解的特定集合稱為“人口”,解中的變量稱為“基因”）,然后采用生物進(jìn)化的過程（如染色體交叉變異淘汰等）不斷提高解的品質(zhì),最后獲得最優(yōu)解。遺傳算法有兩個(gè)重要控制參數(shù)——交叉率Ｐｃ和變異率Ｐｍ對算法的收斂速度有較大影響,文獻(xiàn)[３]采用確定不變的Ｐｃ和Ｐｍ而本文采用隨世代數(shù)增加而不斷自動(dòng)調(diào)整的Ｐｃ和Ｐｍ。這樣做的目的在于：在進(jìn)化的初期,人口的差異一般較大,交叉率大和變異率小有助于加快收斂,而在進(jìn)化的后期,交叉率小和變異率大有助防止過早陷入局部最優(yōu)點(diǎn)。公式如下：

Ｐｃ(ｇｅｎ)＝Ｐｃ(ｇｅｎ－１)－[Ｐｃ（０）－０．３]／ＭＡＸＧＥＮ

Ｐｍ（ｇｅｎ）＝Ｐｍ（ｇｅｎ－１）＋[０．３－Ｐｍ（０）／ＭＡＸＧＥＮ

其中,ｇｅｎ表示世代數(shù),ＭＡＸＧＥＮ表示最大世代數(shù),具體算法如下：

第１步,全局參數(shù)設(shè)定

給出ＰＯＰ＿ＳＩＺＥ（人口數(shù)）、Ｐｃ（０）、Ｐｍ（０）、ＭＡＸＧＥＮ和設(shè)計(jì)次數(shù)ｄｃｎｔ的大小或范圍。

第２步,人口的產(chǎn)生及初使化

設(shè)世代數(shù)ｇｅｎ＝１。以設(shè)計(jì)參數(shù)為變量,組成矩陣Ｘ＝[Ｘ１,Ｘ２,．．．,Ｘｎ]。第一代人口由ＰＯＰ＿ＳＩＺＥ個(gè)染色體構(gòu)成,每個(gè)染色體的基因（即設(shè)計(jì)參數(shù)）在參數(shù)各自取值范圍內(nèi)隨機(jī)產(chǎn)生。

第３步,染色體評價(jià)

為了評價(jià)代世代中染色體Ｘ的優(yōu)劣,建立染色體適應(yīng)性評價(jià)函數(shù)ｅｖａｌ（Ｘ）：

ｅｖａｌ（Ｘ）＝｛F（X,T,S,U）;當(dāng)X滿足約束條件 M,M為一大正數(shù);當(dāng)X不滿足約束條件

對本問題,評價(jià)函數(shù)越小越好。