數字下變頻(DDC)中坐標變換模塊的ASIC實現

1．引言

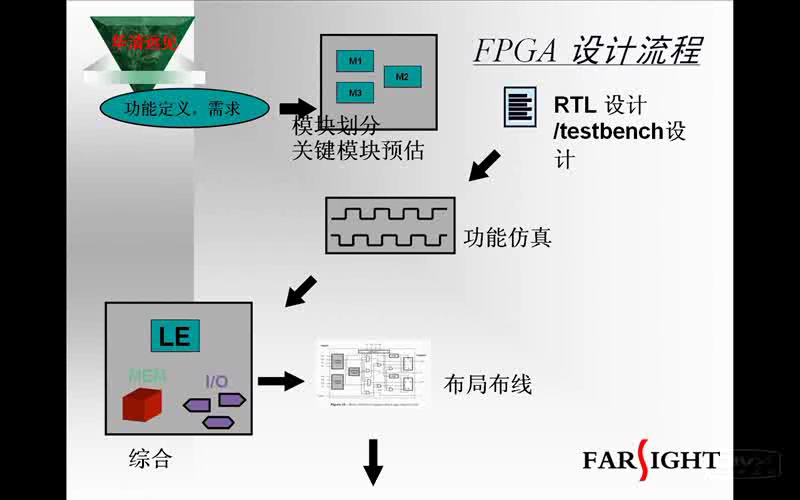
數字下變頻(DDC)技術是軟件無線電接收機的核心技術。其基本功能是從輸人的寬帶高速數字信號中提取所需的窄帶信號，將其下變頻為數字基帶信號，并轉換成較低的數據率，以供后續的DSP作進一步的處理。目前許多型號的DDC芯片事實上其功能己遠遠不只是下變頻，還包括了成形濾波器、定時同步內插濾波器、重采樣NCO、坐標變換、數字ACC等功能，其結構如圖1所示。

CORDIC(Coordinate Rotation Digital Computer)是一種迭代算法，它提供了計算三角函數和欠量求模的方法。該算法僅利用加法和移位兩種運算通過迭代方式進行矢量旋轉，因此，它非常適合于硬件A-SIC實現。本文所要闡述的就是基于CORDIC算法的數字下變頻器中坐標變換模塊的ASIC實現結構，該模塊的主要功能是實現直角坐標系到極坐標系的變換，從而求得由I路信號和Q路信號構成的向量的幅度值和相位值，將得到的幅度信息返回給前級的數字AGC進行增益控制，還可以實現對FM信號的解調。

2．CORDIC算法與實現

2.1 CORDIC算法原理

CORDIC是一種迭代算法，它可以用來計算sin，cos等三角函數，計算幅值和相位等到所需的精度，CORDIC算法計算幅值和相位的原理如下：

假設直角坐標系內有向量A(Xn，Yn)，向量A順時針旋轉θn后得到向量B(Xn，Yn)，如圖2所示。

向量A和向量B之間存在以下關系，用矩陣表示為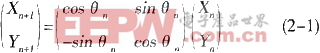

將cosθn提出以后得到

在這里我們取0i=arctan(1/2i)，所有迭代的總和為，其中Si={-1，+1}，則tanθi=Si2-i，可得

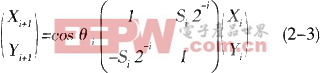
上式Si中的符號決定了向量的旋轉方向，當時Yi≥0，Si=1，順時針旋轉；當Yi0時，Si=-1，逆時針旋轉，式中的cosθi=cos(arctan(1/2i)，隨著迭代次數的增加它收斂于一個常數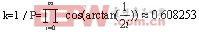，我們暫不考慮這個常數增益，這樣式(2-3)就變為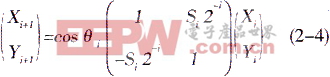

設總共旋轉的角度為，初值為0，則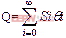，給定向量 一組初值如下

從上面的式子可以看出，當向量A旋轉到X軸時，可以得到迭代的結果為 ，即可求得向量A的幅值和相位。由式(2-4)可知每次旋轉的角度的正切值都是2的負冪次，在硬件實現時只需要執行右移和相加運算就可以實現每次迭代，易于硬件的實現。

2.2 用CORDIC算法的流水結構實現坐標變換

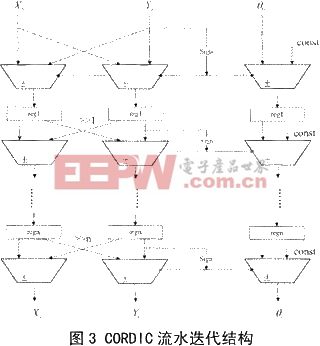
CORDIC迭代結構如圖3所示，采用流水結構每次迭代完成一次旋轉，每級迭代都用寄存器寄存，這樣每個時鐘周期都可以計算出一次幅度和相位。迭代的次數越多，精度越高，當然耗費的資源也就越多。