基于RSSI測距和距離幾何約束的節(jié)點定位算法
Cayley-Menger行列式及距離幾何約束
本文引用地址:http://www.104case.com/article/109140.htm距離幾何理論中,Cayley-Menger行列式可以被用來處理不變空間的歐拉距離幾何問題[6,7]。兩個n點序列{ P1,…,Pn }和{ q1,…,qn }∈ Rm組成Cayley-Menger矩陣,且定義為:
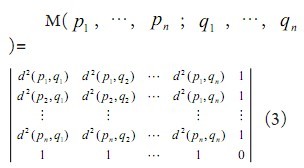
其中,(i,j {1, …,n}為pi點和qj之間的歐式距離。兩個n點序列的Cayley-Menger行列式定義為:
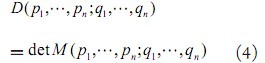
當兩個序列相同時![]()
![]() ,
, ![]() 被稱為Cayley-Menger行列式。在RSSI測距過程中,由于多徑、繞射、障礙物等因素,不可避免出現(xiàn)測距誤差,設(shè)未知節(jié)點與錨節(jié)點之間的真實距離與測量距離。設(shè)未知節(jié)點接收到錨節(jié)點 的測量信息,根據(jù)節(jié)點集合
被稱為Cayley-Menger行列式。在RSSI測距過程中,由于多徑、繞射、障礙物等因素,不可避免出現(xiàn)測距誤差,設(shè)未知節(jié)點與錨節(jié)點之間的真實距離與測量距離。設(shè)未知節(jié)點接收到錨節(jié)點 的測量信息,根據(jù)節(jié)點集合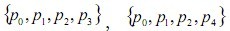 ,…,
,…,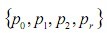 結(jié)合[3]利用Cayley-Menger行列式的經(jīng)典理論的推導(dǎo),可得到r-2個獨立的二次距離約束等式,
結(jié)合[3]利用Cayley-Menger行列式的經(jīng)典理論的推導(dǎo),可得到r-2個獨立的二次距離約束等式,![]() 。
。 ![]() 作為未知節(jié)點與錨節(jié)點在測量過程中出現(xiàn)的誤差,在距離約束限制下形成平方誤差最小化非線性問題:
作為未知節(jié)點與錨節(jié)點在測量過程中出現(xiàn)的誤差,在距離約束限制下形成平方誤差最小化非線性問題:
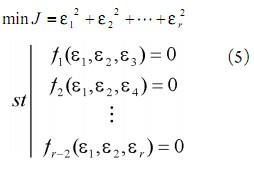
運用數(shù)值分析方法,求得最優(yōu)解 ![]() ,進而得到未知節(jié)點與錨節(jié)點位置估計值:
,進而得到未知節(jié)點與錨節(jié)點位置估計值:
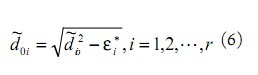
三角形質(zhì)心定位算法模型
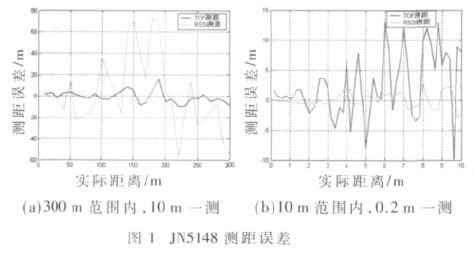
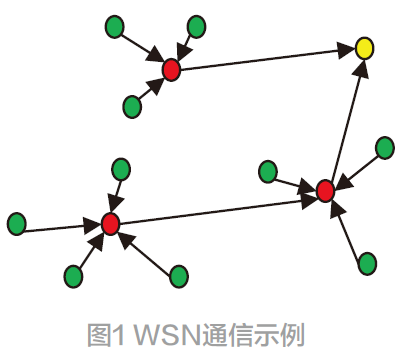
本文研究了未知節(jié)點與其無線射程范圍內(nèi)的三個錨節(jié)點之間的通信約束和幾何關(guān)系得出了未知節(jié)點所在三角區(qū)域,將三角形的質(zhì)心作為未知節(jié)點的估計位置[8,9] 。這里的三角形質(zhì)心定位算法的基本思想是:三個錨節(jié)點A、B、C,未知節(jié)點D,利用RSSI和距離幾何約束算出節(jié)點A和D的距離為;節(jié)點B和D的距離為;節(jié)點C和D的距離為。分別以A、B、C為圓心rA,rB,rC , 為半徑畫圓,可得錨圓交疊區(qū)域,通過計算三個錨圓交疊區(qū)域的三個特征點的坐標,以這三個點為三角形的頂點,未知點即為三角形的質(zhì)心(如圖1所示)。
假設(shè)已知3個錨節(jié)點的坐標分別為A(Xa,Ya) 、B(Xb,Yb) 、C(Xc,Yc) ,與未知節(jié)點的距離分別為rA,rB,rC ,通過下面的公式求出。
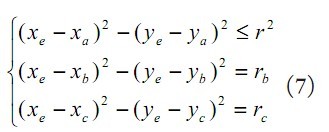






評論