一種基于協(xié)同演化算法的無線傳感器網(wǎng)絡(luò)拓撲設(shè)計方法
0 引言
如今,無線傳感器網(wǎng)絡(luò)(WSN)因其高度認可的實用價值而迅速發(fā)展。為了不斷提高WSN 的相關(guān)技術(shù)和應(yīng)用潛力,進行了各種研究和開發(fā)。例如,WSN 可用于連續(xù)傳感,事件檢測,位置傳感等[1]。WSN 由低成本,低功耗的多功能傳感器組成,其中每個傳感器的尺寸都很小,并且在短距離內(nèi)不受限制地通信。傳感器能夠檢測特定的環(huán)境參數(shù)、信息處理和無線通信。但是,每個傳感器節(jié)點只能進行有限數(shù)據(jù)量的處理。
以前,傳感器網(wǎng)絡(luò)由連接到中央處理站的少量傳感器節(jié)點組成。在大多數(shù)情況下,要監(jiān)測的環(huán)境沒有現(xiàn)有的基礎(chǔ)設(shè)施來提供能源或通信渠道。因此,如何在小而有限的能源上生存并通過無線通信信道進行通信成為WSN 設(shè)計的必要條件[2]。換句話說,WSN 的能耗、覆蓋范圍和最短路由路徑是WSN 設(shè)計過程中的關(guān)鍵問題。
如果每個傳感器將消息直接傳輸?shù)街行墓?jié)點,由于傳感器和中心節(jié)點之間的距離較長,可能會非常耗電[3]。然而,由于傳感器體積小且儲能容量有限,傳感器很難將收集信息有效地直接中繼到中心節(jié)點。在這種情況下,所有傳感器都需要直接或間接地將其數(shù)據(jù)傳輸?shù)街行墓?jié)點,通信信號在傳感器通信半徑范圍內(nèi)與其他傳感器節(jié)點進行通信[4]。最小化通信距離且平衡每個節(jié)點工作負載的設(shè)計可以延長整體網(wǎng)絡(luò)生命周期[3]。
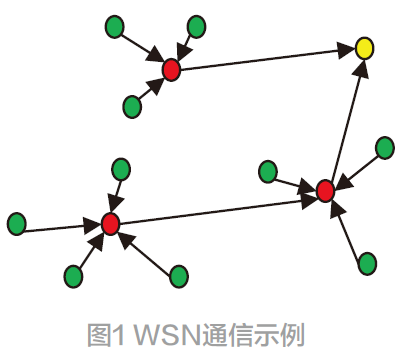
如圖1 所示,WSN 已解決節(jié)能問題,還滿足了其他條件,如負載平衡、容錯等。在 WSN 中,節(jié)點使用集中或分布式方法成為多個集群。傳感器檢測到和收集的數(shù)據(jù)通過所選集群的中心節(jié)點路由的最優(yōu)路徑傳輸?shù)骄W(wǎng)絡(luò)中心節(jié)點[5]。
與直接與中心節(jié)點進行通信相比,集群的形成可以大大降低通信成本。因為功耗與傳輸距離成正比,并且在集群形成中,傳感器節(jié)點將數(shù)據(jù)發(fā)送到最近的集群中心節(jié)點(主節(jié)點),而不是直接發(fā)送到可能更遠的網(wǎng)絡(luò)中心節(jié)點[6]。對于那些遠離中心節(jié)點的主節(jié)點,直接通信是不合適的。我們必須找到最短路由路徑,必須考慮每個節(jié)點的路徑距離和工作負載。
最優(yōu)路由路徑是對WSN 性能有重大影響的最重要的設(shè)計問題之一[7-8]。最短路徑問題(SPP)是一個經(jīng)典的網(wǎng)絡(luò)優(yōu)化問題。最短路由路徑問題的搜索算法有很多,如Dijkstra 算法、Bellman-Ford 算法等。這些算法專為單目標 SPP 設(shè)計。然而,多目標SPP(MSPP)是一個NP 難題。MSPP 可以表述為一個用于查找包含指定源節(jié)點和目標節(jié)點的最小成本路徑,MSPP 是許多設(shè)計和規(guī)劃中出現(xiàn)的經(jīng)典組合優(yōu)化問題[9]。
遺傳算法(GA)具有很強的并行搜索能力,是多目標優(yōu)化問題中最有前途的算法之一。GA 和其他相關(guān)的進化算法可以解決MSPP 問題,并且它們已成功用于各種實際應(yīng)用。在本文中,我們使用擴展的GA 方法來解決WSN 拓撲設(shè)計問題。與其他方法相比,本文提出的方法可以在更短的時間內(nèi)獲得一組近似最優(yōu)解。
1 背景與實際工作
目前,已經(jīng)有不少專家進行了研究來改進WSN 設(shè)計。Kumar 等人[10]旨在提取具有最小能耗的WSN 的最佳集群數(shù)。盡管他們采用的分析方法與預(yù)測結(jié)果一致[11],但他們對集群頭節(jié)點到中心節(jié)點的平均距離做出了過于嚴格的假設(shè)。
Si [12] 提出了一種用于不同數(shù)據(jù)傳輸路徑排列的梯度擴散算法,該算法側(cè)重于平衡傳輸路徑上傳感器節(jié)點的工作量,并提高所有傳感器節(jié)點的預(yù)期壽命。該算法記錄可用于構(gòu)建整個傳輸路徑每個路徑段的節(jié)點數(shù)。通過計算找到最優(yōu)路徑,而且可以降低整體能耗。仿真結(jié)果表明,與其他傳統(tǒng)算法相比,所提算法節(jié)能13.61%。此外,該算法平衡了各傳感器節(jié)點的負載,降低了能耗,使數(shù)據(jù)包能夠快速發(fā)送到最終目的節(jié)點。
Chang 和Ramakrishna[13]提出了一種遺傳算法方法來解決最短路徑路由問題。他們使用可變長度的染色體及其基因來編碼。在位置無關(guān)的交叉位點交換部分染色體,突變操作保持了種群的遺傳多樣性。這個算法可以通過簡單的修復(fù)功能治愈所有不可行的染色體。
如上所述的WSN 工作很少關(guān)注多重目標方面的問題。本文的方法使用 EA 來確定集群頭和路由路徑的數(shù)量和位置,從而最大限度地減少WSN 中的通信距離。
2 建模
通過將WSN 組織成集群形式,可以大大縮短總通信距離,從而節(jié)省能源并延長每個節(jié)點的預(yù)期壽命,均衡主節(jié)點的負載。
2.1 定義參數(shù)
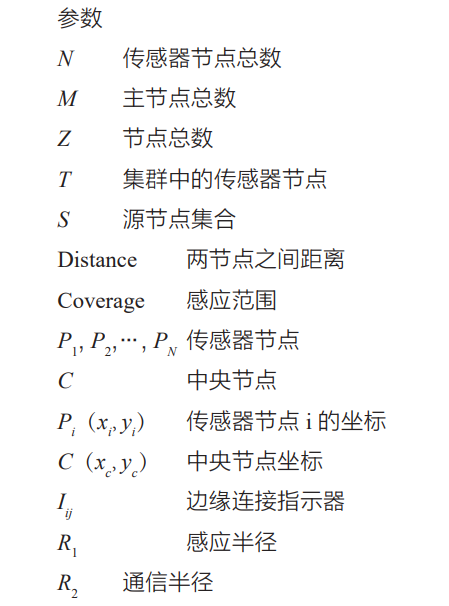
在本文中,我們假設(shè)WSN 要監(jiān)測的區(qū)域是一個平坦的方形表面,并且每個傳感器節(jié)點都可以檢測由傳感器半徑確定的圓形區(qū)域內(nèi)的所有數(shù)據(jù)。所有傳感器節(jié)點都是相同的,并且在部署在唯一的坐標上后,坐標是固定不變的。WSN 模型的參數(shù)和變量定義如下:


2.2 數(shù)學(xué)模型
為了模擬WSN設(shè)計問題,我們定義了一個有向圖,其中V 是一組M 個主節(jié)點,E 是一組邊。每個節(jié)點的負載對應(yīng)一個非負,并表示節(jié)點k 和節(jié)點m 之間的距離。如果節(jié)點k 和節(jié)點m 之間的距離小于通信半徑,則節(jié)點k 和節(jié)點m 之間存在邊。主節(jié)點最大覆蓋、最小總距離和最佳路由路徑的數(shù)學(xué)模型表述如下:
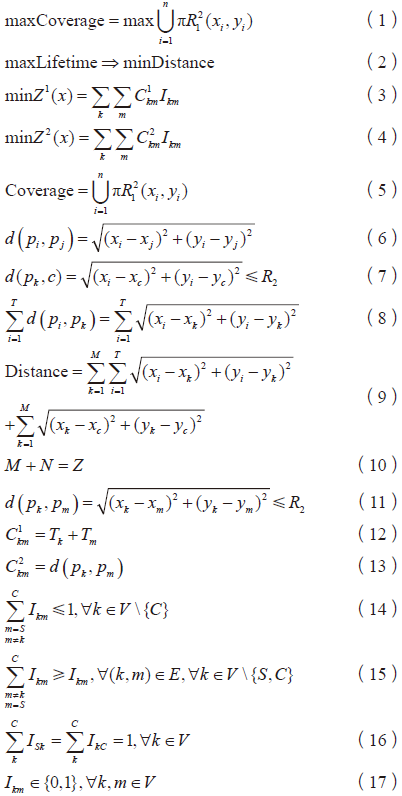
等式(6)是兩個節(jié)點之間的距離,它必須小于通信距離,約束(7)確保每個主節(jié)點與中心節(jié)點之間的距離在通信距離限制范圍內(nèi),式(8)是集群中節(jié)點之間的總距離,式(9)是整個網(wǎng)絡(luò)的總距離,約束(10)保證主節(jié)點數(shù)和傳感器節(jié)點數(shù)等于節(jié)點總數(shù)。式(11)是兩個主節(jié)點之間的距離。式(14)和式(15)確保除源節(jié)點和目標節(jié)點外,每個節(jié)點不存在或只有兩條相鄰邊。約束(16)和式(17)確保結(jié)果是源節(jié)點和目標節(jié)點之間沒有環(huán)路的路徑。
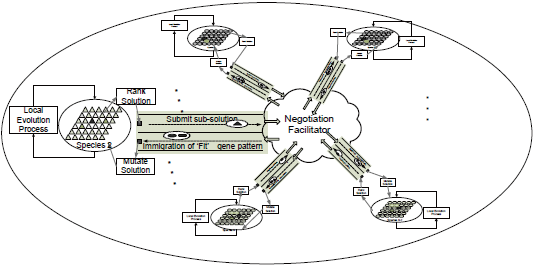
圖2 生態(tài)系統(tǒng)中的可協(xié)商進化算法
3 協(xié)同演化算法
EA 是一種啟發(fā)式優(yōu)化方法,靈感來自生物物種遺傳特征的自然進化過程[11]。EA 在為多目標問題找到最佳解決方案方面無效,但它可以快速收斂,找到最優(yōu)的解決方案。在本文中,我們使用可協(xié)商進化算法[14] 來解決多目標WSN 布局問題。NEA 過程如圖2 所示,生態(tài)系統(tǒng)可用于表示W(wǎng)SN 的整體性能,并且生態(tài)系統(tǒng)中物種的進化可用于對相應(yīng)子問題的進行求解,優(yōu)化算法進行建模。
首先將WSN 問題劃分為N 個子問題,每個問題都可以通過EA 更有效地解決。進行進化過程后,選擇一些解決方案作為跨物種進化候選者,然后評估每個子解決方案對系統(tǒng)目標的貢獻。從本質(zhì)上講,可以識別顯著能提高系統(tǒng)目標適應(yīng)性的基因模式,并在合作伙伴之間共享信息。最優(yōu)的基因模式可能會在EA 模型之間遷移,以促進對整體解決方案的合理探索,從而避免重復(fù)收斂到局部目標,然后重新啟動每個EA 模型的演變并迭代該過程,直到滿足終止標準。[14]
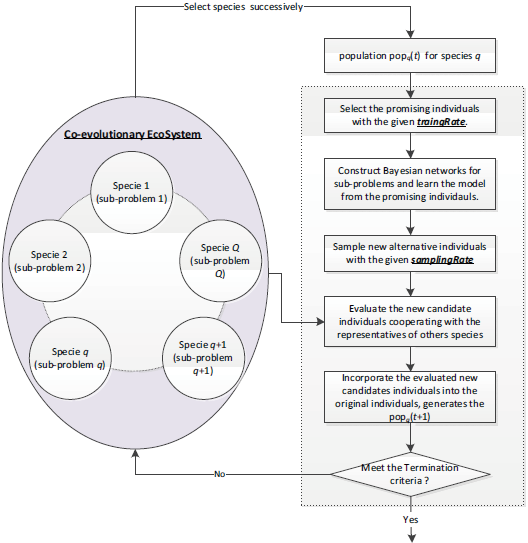
圖3 NEA優(yōu)化結(jié)果
本文采用合作貝葉斯優(yōu)化算法(COBOA)實現(xiàn)協(xié)商促進。圖3 描述了每個物種的每個迭代器使用任何標準的進化算法,從原始種群中選擇有較優(yōu)的解決方案。首先,構(gòu)建一個用于對子問題進行建模的貝葉斯網(wǎng)絡(luò),獲得最優(yōu)的解決方案。然后,使用構(gòu)建的網(wǎng)絡(luò)對一些新的候選個體進行采樣,新的候選個體與其他種群的代表合作。最后,將評估的新候選個體納入原始種群。該過程將迭代,直到滿足預(yù)定義的終止條件。[16]
4 實驗與分析
在本文中,NEA 和CEA(交叉EA-baesd)[15] 都是在Eclipse 環(huán)境下使用JAVA 語言編程的。該程序在配置有2.33 GHz CPU 和2.00 GB RAM 的PC 上運行。
圖4 顯示了當中心節(jié)點位于(0,0)時NEA 的優(yōu)化結(jié)果。
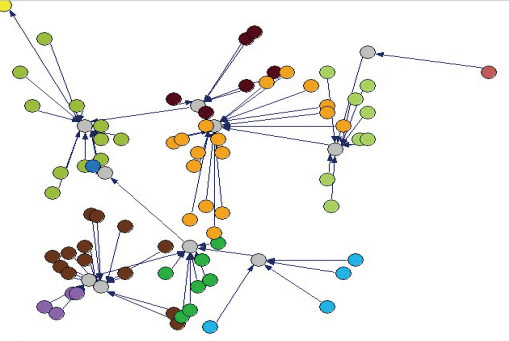
圖4 NEA優(yōu)化結(jié)果
從圖5 和圖6 中,我們可以看到NEA 方法取得了更好的結(jié)果。圖5 顯示了與CEA 相比,NEA 發(fā)現(xiàn)更短的總通信距離值,圖6 分別顯示了NEA 和CEA 實現(xiàn)的覆蓋值曲線。
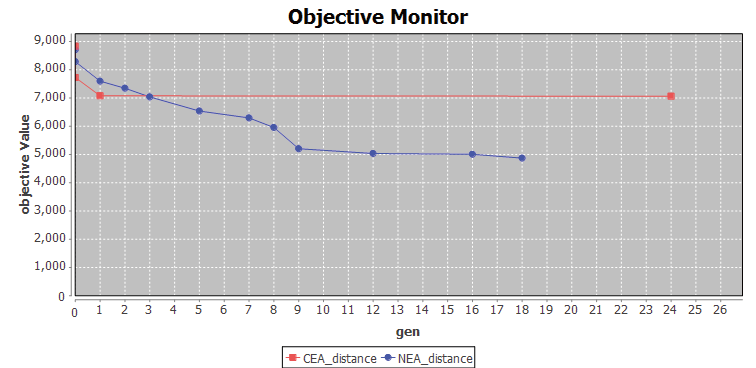
圖5 距離值曲線
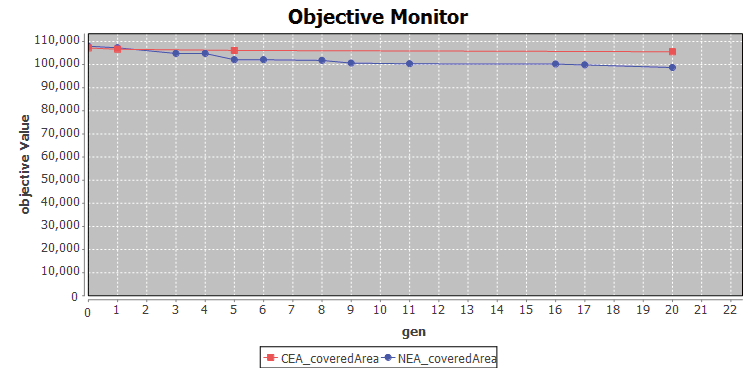
圖6 覆蓋值曲線
5 結(jié)束語
本文提出了一種NEA方法來解決多目標優(yōu)化問題,例如確定WSN 的布局和路由策略。實驗表明,NEA 在復(fù)雜環(huán)境下提供的決策是有效的。在我們未來的工作中,作者希望改進談判促進者,以解決建模和解決復(fù)雜多目標問題。基于所提出的方法,作者還希望及時實現(xiàn)一個功能齊全的軟件應(yīng)用程序,用于設(shè)計真實案例場景的WSN。
參考文獻:
[1] 汪清清,王茜,李小平.網(wǎng)絡(luò)環(huán)境下數(shù)據(jù)交換方案的設(shè)計與實現(xiàn)[J].東南大學(xué)學(xué)報(自然科學(xué)版).2007(4):59-66.
[2] ARCHANA B, VIJAY A S P. Sensor networks: an overview[J].University of California, Davis, CA 95616.
[3] 楊平,鄭金華.遺傳選擇算子的比較與研究[J].計算機工程與應(yīng)用,2007(15):37-46.
[4] NAVID A, ALIREZA V, XU W Y, et al. Cluster size optimization in sensor networks with decentralized clusterbased protocols [J]. Computer Communications, 2012(35):207-220.
[5] NAVID A, ALIREZA V, XU W Y, et al. Cluster size optimization in sensor networks with decentralized clusterbased protocols [J]. Computer Communications, 2012(35): 207-220.
[6] W. STALLING. High-Speed Networks: TCP/IP and ATM Design Principles[J]. Englewood Cliffs, NJ: Prentice- Hall,1998.
[7] M. K. ALI, F. KAMOUN. Neural networks for shortest path computation and routing in computer networks[J]. IEEE Trans. Neural Networks, 1993,4(11):941–954.
[8] 董紅斌,丁蕊.協(xié)同演化算法及其應(yīng)用[M].哈爾濱:哈爾濱工程大學(xué)出版社,2021.
[9] D. KUMAR, C.A. TRILOK, R.B. Patel. EEHC: energy efficient heterogeneous clustered scheme for wireless sensor networks[J]. Computer Communication, 2009,32 (4) :662-667.
[10] W.B. HEINZELMAN, A.P. CHANDRAKASAN, H. BALAKRISHNAN, An application-specific protocol architecture for wireless micro-sensor networks[J]. IEEE Transactions on Wireless Communications, 2002 (4) : 660-670.
[11] 何俊輝, 潘正祥.“梯度擴散算法”2011年信息技術(shù)與應(yīng)用學(xué)術(shù)會議[C],2011.
[12] CHANG W A, R. S. RAMAKRISHNA. A genetic algorithm for shortest path routing”, IEEE transactions on evolutionary computation[J]. 2002,6(12):566-578.
[13] HAO X, LIN H W, T MURATA. Application of negotiable evolutionary algorithm in flexible manufacturing planning and scheduling[C]. Proceedings of 17th International Conference on Industrial Engineering and Engineering Management (IE&EM 2010)
[14] 張麗,林文浩. 基于種群交叉策略遺傳算法的無線傳感器網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計[D].哈爾濱:哈爾濱工業(yè)大學(xué),2012.
[15] HAO X, CHEN X, LIN H W, et al. Cooperative bayesian optimization algorithm: a novel approach to simultaneous multiple resources scheduling problem[C]. Second International Conference on Innovations in Bio-inspired Computing and Applications, 2011.
(本文來源于《電子產(chǎn)品世界》雜志2023年4月期)








評論