通俗易懂的Harris 角點檢測

Harris 角點檢測 認為 特征點具有局部差異性。

如何描述“特征點具有局部差異性”：

以每一個點為中心，取一個窗口，窗口大小為5*5或7*7像素大小。

這個窗口描述了這個特征點周圍的環境。

如果這個特征點具有局部差異性，那么以這個特征點為中心，把窗口向360度任意一個方向移動，窗口的變化比較大，則這個特征點的周圍環境變化比較大。

數學公式：

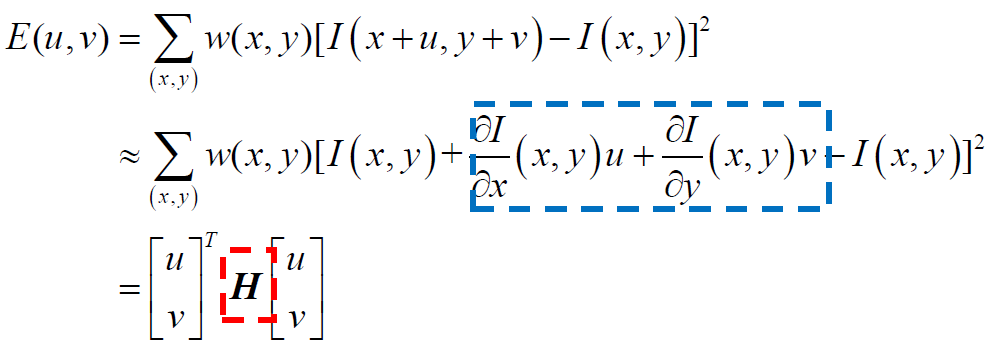
（x,y）：表示像素的位置。

：表示窗口內的每個像素。

w(x,y)：表示 這個位置的權重。

若w=1，則說明窗口中所有的像素貢獻是一樣的。

若w設置為以這個特征點為中心的高斯，

高斯權重，說明距離這個特征點越近，權重越大；越往周圍發散，權重越小。

I(x,y)：表示(x,y)這個位置的像素值。如果是灰度圖，I就是灰度值，如果是彩色圖，I就是RGB值。

u和v表示窗口移動的方向。

I(x+u,y+v) - I(x,y)：表示對應像素的灰度差異。

：在整個窗口內，即在局部環境內求這個像素灰度差異的加權和。

對 I(x+u,y+v) - I(x,y)進行一階泰勒展開，得到

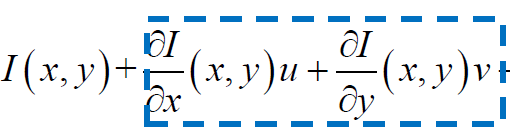
在(x,y)處的灰度值，再加上u方向和v方向的偏導數。

整理后，結果為：

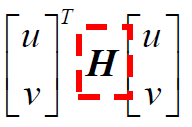
u和v表示窗口移動的方向， H表示Harris矩陣，主要由圖像梯度表示。

對Harris矩陣進行特征分解：

得到兩個特征值，矩陣的這兩個特征值反映了：兩個相互垂直的方向上的變化情況。

一個是變化最快的方向，一個是變化最慢的方向。

前面設置了u和v，這是兩個向量，表示窗口移動的方向。以(x,y)這個點為中心，進行360度的旋轉。

特征值對應的特征向量，確定了變化最快的方向和變化最慢的方向。其他方向的變化情況，介于這兩者之間。

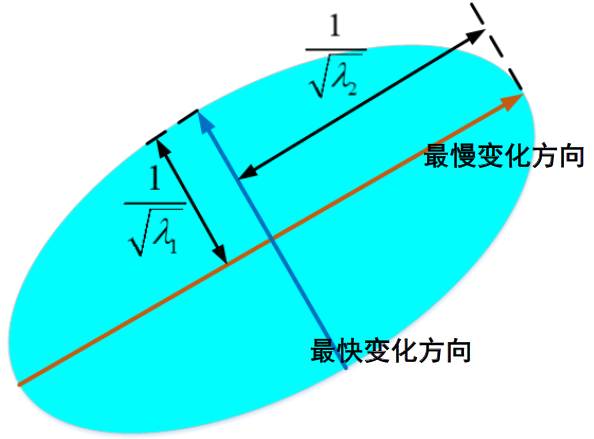
通過對Harris矩陣的分析，得到如下結論：

只有當Harris矩陣的兩個特征值都非常大的時候，特征點才能和周圍環境區別比較大，是我們想要的特征點。

現在檢測特征的任務就變成了，計算Harris矩陣，并判斷其兩個特征值的大小。

Harris角點準則

實際中，并不對Harris矩陣進行分解求其特征值，因為計算量太大。而是使用Harris角點準則。

C = Harris矩陣的行列式值 – k(Harris矩陣的跡)2

Harris矩陣的行列式值：Harris矩陣特征值的乘積

Harris矩陣的跡：Harris矩陣特征值的和

·  k的值越小，檢測子越敏感。k的值越小，能檢測到的特征點越多。

·  只有當和同時取得最大值時， 才能取得較大值。

·  避免了特征值分解，提高檢測計算效率。

本文僅做學術分享，如有侵權，請聯系刪文。