嵌入式音頻處理基礎(二)

定點運算

　　執行定點運算的處理器一般對信號使用二進制補碼表示法。定點格式可以表示有符號和無符號的整數和分數。在定點處理器上使用有符號的分數格式是在數字信號處理中最常見的。整數與分數格式的差別在于二進制小數點的位置。對于整數，二進制小數點是在最低位的右邊；而對于分數，通常把它們的小數點放在符號位的右邊 。圖4a表示了整數和分數的格式。

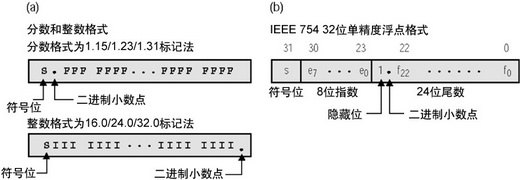
圖4(a)分數和整數格式  (b)IEEE 754 32位單精度浮點格式

　　雖然定點的規則簡化了數值操作且節省了存儲器，但同時也存在動態范圍和精度之間的折衷。在需要保持很高分辨率同時又要使用很大數值范圍的應用場合，就需要使用一個可以根據幅值和指數而移動的小數點。

浮點運算

　　使用浮點格式就可以在同一系統中表示非常大和非常小的數。浮點數與有理數的科學記數法十分相似。浮點數是用尾數和指數描述的。尾數確定了精度，而指數控制著動態范圍。

　　有一個標準管理著數字機的浮點運算。這個標準叫IEEE-754(圖4a)；對于32位浮點數可以歸納如下。第31位(MSB，最高位)是符號位，它的0表示符號為正，它的1表示符號為負。從第30位到第23位是表示2的整次冪的指數字段(exp_field)，并以127作為偏移量。最后，第22位到第0位表示分數的尾數(mantissa)。隱藏位一般是指在小數點的左邊有一個1。

　　32位的IEEE浮點數的值可以用下面的等式來表示：

　　(-1)sign_bit × (1.mantissa) * 2(exp _field-127)

　　依靠8位的指數和23位的尾數，IEEE-754達到了動態范圍和精度之間的一個平衡。而且，IEEE浮點庫還包括了對于像??、0和NaN(不是一個數)等附加特性的支持

　　表3表示了從常用的浮點和定點類型可以達到的最小數和最大數。

表3  各種數據格式的動態范圍比較

在16位架構上的仿真

　　正如我們在前面解釋的，16位處理并不能為高質量音頻提供足夠的SNR，但這并不是說您不應該選用16位處理器作為音頻系統。例如，用一個32位的浮點機把一個算法編寫成保持原來32位數據風格的程序，是比較容易的；但一個16位處理器也可以通過非常低成本的仿真而保持32位的完整性。圖5示出了為一個嵌入式算法選擇數據類型時的一些可能性。

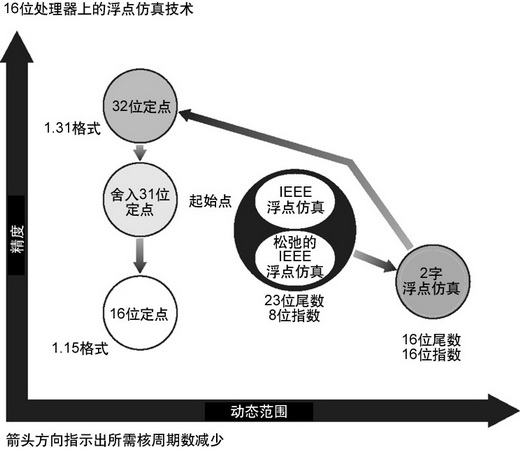
圖5  根據一個應用的目標，可以有許多滿足系統要求的數據類型

　　在本節的余下部分，我們將描述如何在一個16位定點機上實現浮點和32位擴展精度定點格式的功能。

在定點處理器上的浮點仿真

　　在大多數的16位定點處理器上，IEEE-754浮點功能是通過對C/C++或匯編語言的庫調用而提供的。這些庫通過使用定點乘法和運算邏輯而對所需的浮點處理進行仿真。這種仿真需要額外的處理周期來完成。但是，當定點處理器內核的時鐘進入到500 MHz - 1 GHz范圍時，在對符合IEEE-754的浮點運算進行仿真時需要的額外周期就不那么重要了。

　　為了降低計算的復雜性，可以使用IEEE-754的“松弛”版。這意味著浮點運算并不會實現像?和NaN這樣一些標準特性。

　　進一步的優化是對尾數和指數使用一個更為本機化的類型。舉個例子，ADI公司的Blackfin定點處理器架構具有一個由十六個16位寄存器組成的寄存器組，而這個寄存器組還可以用作8個32位寄存器。在這種配置下，每個內核時鐘周期內，兩個32位寄存器可以從全部四個半寄存器中獲取操作數。為了優化Blackfin寄存器組的使用，可以使用一種雙字的格式。這樣，一個字(16位)被保留為用作指數，而另一個字(16位)則保留給分數部分使用。

雙精度定點仿真

　　對于許多應用來說，16位定點數據是不夠的，如果使用仿真浮點運算，那么計算量又太大。對于這些應用，擴展精度定點仿真也許足以滿足系統的要求。使用一個高速定點處理器將確保有效降低所需的計算量。音頻中兩個常用的擴展精度格式是32位和31位定點表示。

32位-精確仿真

　　32位運算是16位定點處理器的自然軟件擴展。對于那些32位寄存器組可以分為16位的兩半而進行存取的處理器來說，這些兩半的寄存器可以合起來用于表示一個32位定點數。Blackfin處理器的硬件結構允許單周期32位加法和減法。

　　例如，當一個32位乘法采用累加器迭代操作時(像我們馬上就要討論的有些算法情況)，我們只需用3個周期內的16位乘法就可以實現32位的精度。兩個32位操作數(R0和R1)中的每一個都可以分為16位的兩半(R0.H / R0.L和R1.H / R1.L)。

　　從圖6可以容易看出，在使用16位乘法器的指令組合來對32位乘法R0 x R1進行仿真的時候，我們需要下面的操作：

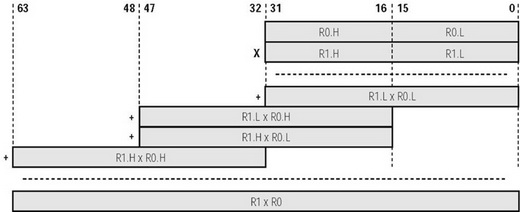
圖6  用16位操作實現32位乘法

　　* 四次16位乘法以產生四個32位結果

　　1. R1.L x R0.L
　　2. R1.L x R0.H
　　3. R1.H x R0.L
　　4. R1.H x R0.H

　　* 三次操作以保持在最終結果中數位的位置(符號>>表示右移)。由于我們正在做分數運算，所以結果是1.63(1.31 x 1.31 = 2.62，帶有一個冗余的符號位)。在大多數情況下，這個結果可以截取到1.31，以便裝入一個32位數據寄存器。因此，乘法的結果應該以符號位為基準，或者以最大有效位為基準。這樣，那些最右邊的最小有效位可以在截取操作時被安全地截取。

　　1. (R1.L x R0.L) >> 32
　　2. (R1.L x R0.H) >> 16
　　3. (R1.H x R0.L) >> 16
　　一個32位乘法的最終表達式
　　((R1.L x R0.L) >> 32 + (R1.L x R0.H) >> 16) + ((R1.H x R0.L) >> 16 + R1.H x R0.H)

　　在Blackfin架構中，這些指令可以并行執行，以實現在三個周期內完成一次32位乘法的有效速率。

31位-精確仿真

　　我們可以把最高要求31位精度的定點乘法的計算時間減少到2個周期。這個技術對于音頻系統特別有吸引力，因為音頻系統通常至少需要24位的表示法，而32位的精度也許有些過分。使用“6 dB規則”，31位的精確仿真仍然保持了大約186 dB的動態范圍，即使考慮了所有的量化效應之后，這仍然具有非常充裕的余量。

　　從圖6中的乘法框圖來看，很明顯的一點是，最小有效位半字的乘法R1.L x R0.L對最終的結果沒有太大的貢獻。事實上，如果把結果截取為1.31，那么這個乘法只影響到1.31結果的最低位。對于許多應用來說，由這一位引起的精度損失是通過減少一次16位乘法、一次移位和一次加法以加速32位乘法而得以平衡的。

　　31位精確乘法的表達式為
　　((R1.L x R0.H) + (R1.H x R0.L) ) >> 16 + (R1.H x R0.H)

　　在Blackfin架構中，這些指令可以并行執行，以實現在2個周期內完成一次32位乘法的有效速率。

　　所以，這是音頻處理中使用的數據格式的“獨家新聞”。在本文的最后一部分，我們將介紹開發嵌入式音頻應用的一些策略，主要聚焦于常用算法中的數據傳輸和構建模塊。