機器人控制系統運動學方程
為了解此系統的反向運動方程,必須確定平臺種類以及執行器匯聚點的位置,因為腳長就是點與點之間的距離。平臺執行器所處位置用基點坐標系表示如下:
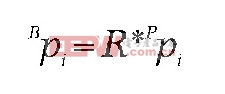
上述等式的下標表明了向量的參考坐標系。這里,點的位置實際上是齊次坐標,以(x, y, z, w) 或者 (x/w, y/w, z/w)的形式表述,為了簡化討論,這里的w我們可以令其等于1。R是變換矩陣,可以將平臺點(Ppi)也就是平臺系數轉換成(Bpi),也就是基座系數。R是3×4的矩陣,包括3×3的旋轉矩陣和3×1的平移矩陣。

在R等式中,“s”代表正弦函數;“c”代表余弦函數。上述等式中的旋轉矩陣是單位矩陣,用來變換roll、pitch和yaw三個向量的方向。平移矩陣就是一個簡單的向量。由于(Bbi)的值是已知的,所以一旦知道了(Bpi)的值,就可以通過計算兩點的距離得到腳的長度。

上面的等式實際上很簡單,但是由于引入了矩陣理論,所以有很多項。下面是最終的反向運動方程(對于腳“i”)。
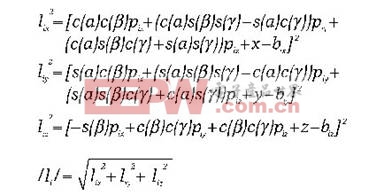
此系統的前向運動學方程相對復雜一些,由于處理上的要求,前向方程也不容易解。這里,比直接解方程更好的方法是使用迭代法,初始估計值代入方程、更新,然后重復,直到估計值的誤差小于某一限定值。具體的計算方法在此就不再贅述,此方法對于以下的過程都可以通用。此方法是前文提及的牛頓迭代法的推廣。關于此方法有很多相關文章,本文在此著重討論前向運動方程的應用。第一步是估計初始姿態K,或者換種說法,估計(α , , γ, x, y, z)的值。對于一個運動控制器,初始估計值通常是(α , , γ, x, y, z)的受控位置。從此估計值,反推運動學方程,可以計算出執行器的長度,稱之為 (g1, g2, g3, g4, g5, g6) ,或者以向量的形式寫成g.,數學表達式如下:g = I(k)。
然后,基于估計值算出的長度與來自反饋設備的實際長度I相比較,得到“估值誤差”e,可以寫成e = g – l。
如果估值誤差小于某一個限定值,那么此過程就此結束。如果估值誤差不小于這個限定值,那么,就需要一個更好的估計值。這個過程一直重復,直到估計值足夠完美(此時,這個估計值就被作為方程的解!)為了理解如何從數學上確定一個“更好的估計值”,首先考慮下面這個簡單的微積分學例子。假設我們有一個通用函數y = f(x),f是非線性的。如果我們要計算由x的變化所導致的y的變化,下面的等式有效:

陀螺儀相關文章:陀螺儀原理









評論