對基于FPGA的高斯白噪聲發生器的研究與設計

　　其典型的功率譜密度如圖2所示。

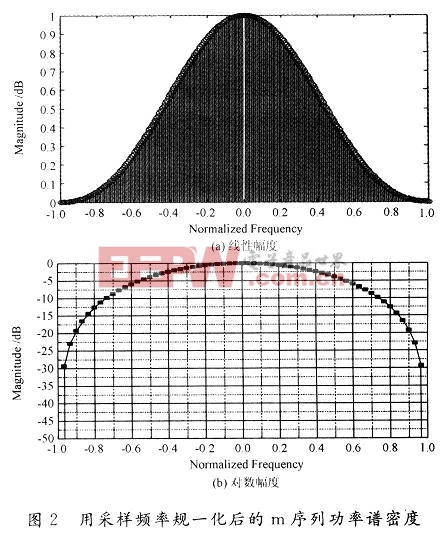
　　由圖2可以看出，m序列的功率譜密度的包絡是[(sin x)/x]2形的，它約在偽隨機序列基本時鐘頻率的45％帶寬內具有均勻功率譜密度，所以用濾波器濾除該頻帶內的信號就可以近似看作帶限白噪聲。m序列的均衡性、游程分布、自相關特性和功率譜與隨機序列的基本性質很相似，所以m序列屬于偽噪聲的序列或偽隨機序列。

　　2．2 FIR數字濾波算法

　　m序列的功率譜是固定的，要生成帶寬可調的數字噪聲序列需要對m序列進行低通數字濾波，本文采用的是FIR數字濾波器。

　　由Lindeberg定理可知，設有獨立隨機變量序列

　　該定理證明了由大量微小且獨立的隨機因素引起，并積累而成的變量，必是一個正態隨機變量。FIR濾波器的單位沖激響應為h(n)，0≤n≤N一1，輸入函數為x(i)，則輸出函數y(i)可以寫為：

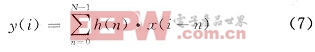
　　該算法需要N次相乘，N-1次累加。為了產生帶寬小于5 MHz高質量的數字噪聲序列，需要構建窄通帶、通帶阻帶轉換迅速的低通濾波器，對此僅僅增加單級FIR濾波的沖激相應長度n是不夠的，對此本文采用了多級FIR數字濾波的方法。為了使得多路多級FIR濾波器能夠在常用FPGA平臺上實現，對FIR數字濾波模型進行算法優化，以節約所需邏輯單元資源是很有必要的。

　　采用單位沖激相應h(n)為偶函數的FIR濾波器，并取階數N為奇數，則式(6)可以化簡為：

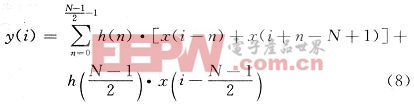
　　采用該方法可以將FIR算法中乘的次數減半，總計算量減為(N+1)／2次相乘，N-2次累加，極大地節省了FPGA的邏輯單元資源。FIR的濾波過程實質上就是一個延遲后加權相加的過程，即濾波輸出y(i)是輸入x(i)以及它的前N一1個狀態的加權疊加。