模數混合型FIR噪聲濾波器設計
一般的相位反饋系統中使用鎖相環通過分頻器的比例關系,可以輸出一個頻率是輸入參考信號N倍的時鐘。由于傳統結構的分頻比只能是整數限制,使得頻率分辨率直接取決于輸入信號頻率。△-∑分數鎖相環通過采用數字調制,實現了分數分頻比,從而可以提供更高精度的頻率分辨率,這為時鐘信號的產生和頻率規劃帶來更大的靈活性。然而,△-∑調制器的使用也引入了量化噪聲,在低過采樣率的環路中限制了帶外相位噪聲性能,需要加以解決。現有的量化噪聲抑制技術仍然需要較大的硬件代價,并設法減小失配等非理想因素才能得到比較好的性能。由此可見,數字FIR噪聲濾除技術具有結構簡單,可靠性高的優點,但存在噪聲增益問題。目前針對這一問題還投有很好的解決辦法,本文結合模擬和數字實現各自的優點,設計出一種混合型FIR噪聲濾波技術,該技術能有效地解決上述問題。
1 電路設計原理
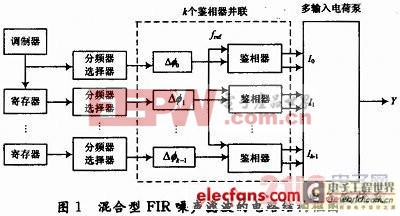
混合型FIR噪聲濾除電路的結構設計如圖1所示。在△-∑鎖相環或△-∑延時鎖定環中,鑒相器輸入端的2個信號之間存在受調制器控制的瞬時相位誤差,電荷泵將這個數字控制的相位誤差轉換為模擬域電荷。為了實現對量化噪聲的FIR濾波功能,結構中采用了多個鑒相器并聯的形式。△-∑調制器的輸出并不像傳統結構中直接去控制分頻器或相位選擇器實現量化操作,而是經過一個寄存器鏈實現一個或數個時鐘周期的延時,并從中選出若干抽頭分別去控制對應的分頻器或相位選擇器,量化所產生的瞬時相位誤差經過各支路鑒相器后在一個多輸入電荷泵中合成為模擬域誤差電荷。
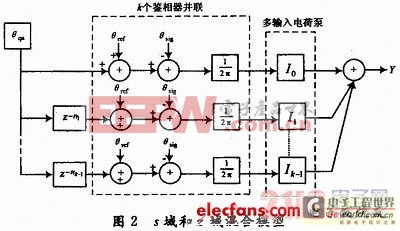
該結構對應的S域和Z域混合模型如圖2所示。經過推導可以得到電荷泵的輸出為:

式中:θref為參考信號相位;θsig為環路返回信號相位;θqn為相位域的量化噪聲;ni為調制器輸出的延時深度,Ii為多輸入電荷泵的各支路電流;fref為鑒相器工作頻率;H(z)為針對量化噪聲的等效FIR濾波的傳遞函數:

電荷泵電流在該結構中扮演了雙重角色。從式(1)可以看出,同常規結構一樣,總電流影響了環路動態特性;另一方面,式(2)表明各支路電流決定了所實現FIR濾波器傳遞函數的各項系數。只要根據所要實現的傳遞函數設置調制器輸出的延時深度以及電荷泵各支路電流的分配比例,就可以實現全定制的噪聲整形。此外,式(2)中當f=0時,將有H(z)≡1。這表明無論設計參數如何選取,該結構所實現的FIR濾波器恒有單位直流增益,因此從根本上解決了現有數字FIR噪聲濾除技術中的噪聲增益問題。
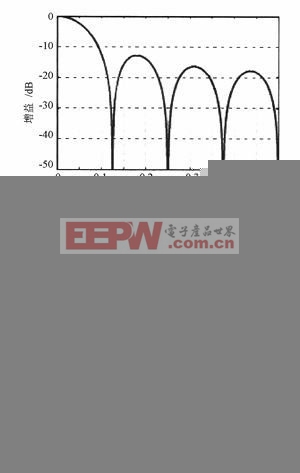
現以8抽頭混合型FIR濾波器為例,分析該結構所實現的全定制噪聲整形。通過采用并行8支路鑒相器和1個8輸入的電荷泵,并給電荷泵各支路分配相同的電流,設置圖1中調制器輸出的每級延遲為單個時鐘周期,可以實現如圖3所示的濾波器頻域響應。對應的傳遞函數為:

圖4是行為級仿真得到的采用混合型FIR濾波器的新結構鎖相環輸出的頻譜,并與傳統結構做了對比。所有模塊均為無噪聲理想模型,因此頻譜中只含△-∑調制帶來的量化噪聲。所用參考時鐘頻率為14.318 MHz;輸出頻率為532 MHz,對應的分頻比為37.156;電荷泵總電流為320μA,對應每個支路40μA;振蕩器增益為250 MHz/V;環路濾波器采用2階;環路帶寬設為700 kHz,對應的過采樣率僅為10;所用調制器為3階MASH結構。圖中橫坐標按照參考時鐘頻率歸一化。對比圖4和圖3可以看出,混合型FIR濾波器按照其傳遞函數實現了預期的對量化噪聲的抑制。
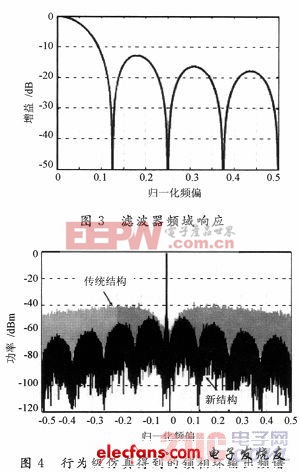
圖5(a)是行為級仿真得到的環路建立過程中振蕩器控制電壓的瞬態波形
分頻器相關文章:分頻器原理











評論