利用噪聲系數度量分析射頻電路中的噪聲

關于射頻模擬設計中的噪聲分析，通過示例了解噪聲系數度量，包括本規范的關鍵方面。

除了一些特定的應用，例如，當需要抖動效果時，噪聲通常是一種不想要的現象。科學家和工程師已經表征了不同電路元件產生的噪聲，并開發了可用于分析電路噪聲性能的方法。在模擬電路設計中，我們通常將噪聲效應建模為輸入參考噪聲電壓和電流源。然而，在射頻（RF）設計中，噪聲系數度量可以是表征電路噪聲性能的更有用的方法。

在本文中，我們將介紹噪聲系數度量，強調該規范的一些微妙之處，最后看一個例子來澄清所討論的概念。

射頻模擬設計中的噪聲分析

我們通常用串聯電壓源來模擬電路中所有噪聲源的影響 ($\overline{v_{n,input}^2}$)

以及并聯電流源 ($\overline{i_{n,input}^2}$)，如圖1所示。

串聯電壓源和并聯電流源電路中噪聲源的影響。

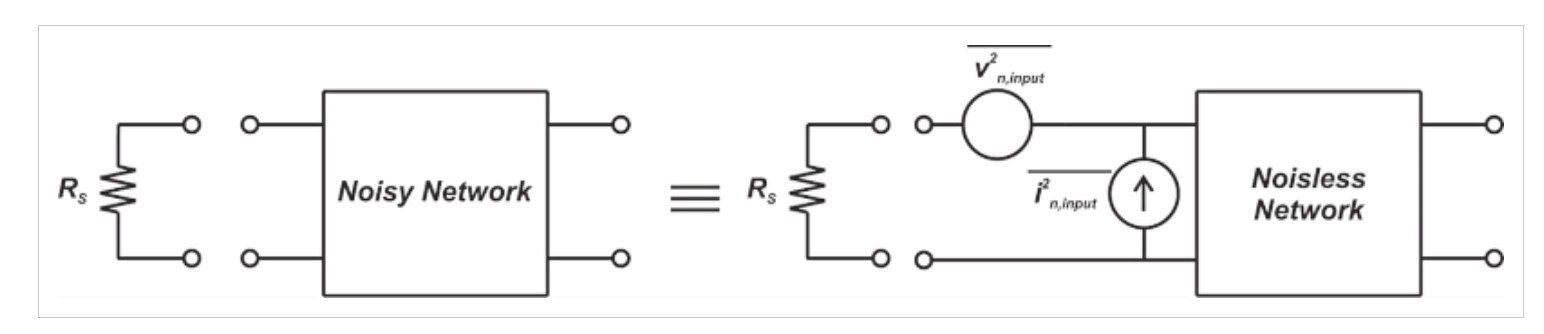
圖1。串聯電壓源和并聯電流源電路中噪聲源的影響。

在圖1中，“無噪聲網絡”與“有噪聲網絡”相同，除了其組件（電阻器、晶體管等）被假設為無噪聲。通過將兩個電路的輸出噪聲相等，我們可以找到輸入參考噪聲電壓和電流源的值。對于任何源阻抗（RS），這兩個輸入發生器對于正確建模線性雙端口網絡的噪聲是足夠和必要的。

使用OP27運算放大器示例了解源阻抗

在射頻設計，特別是離散射頻設計中，我們通常更喜歡使用噪聲系數概念，而不是噪聲電壓和電流源模型。然而，上述模型可以幫助我們更好地理解電子電路中的噪聲行為和噪聲系數度量的微妙之處。

一個關鍵的觀察結果是，電路的輸出噪聲取決于前級的輸出阻抗（或源阻抗，RS）。這可以通過考慮RS=0和RS趨于無窮大（RS→∞）的極端情況來理解，

 RS = 0, $\overline{i_{n,input}^2}$

是短路，對輸出噪聲沒有影響。

另一方面如果RS趨于無窮大，

 $v_{n,input}^2$ 

不能產生輸出噪聲。圖2顯示了源極電阻（R）對實際運算放大器（OP27）配置的影響。

源極電阻對OP27運算放大器配置的影響。

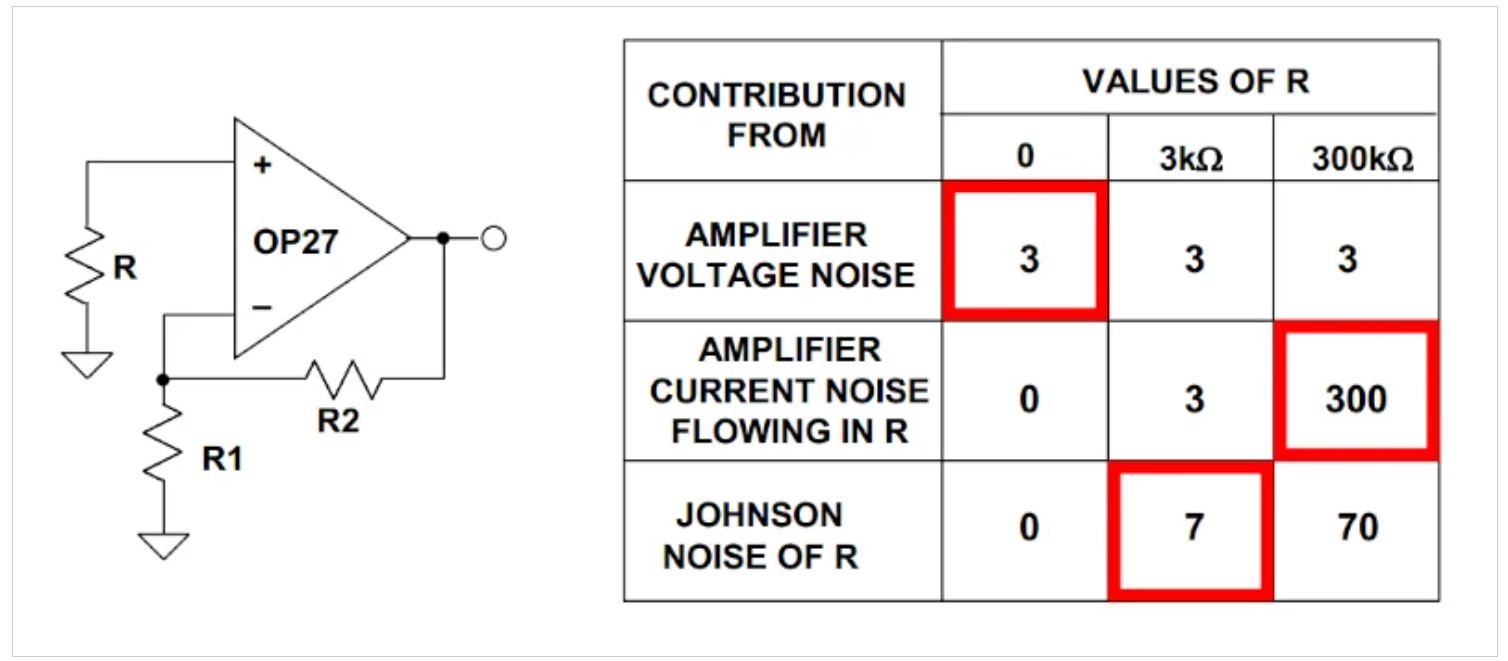
圖2:源極電阻對OP27運算放大器配置的影響。圖片由ADI公司提供

OP27的電壓噪聲為

 $3\frac{nV}{\sqrt{Hz}}$ 

在上述示例中，僅考慮了來自源阻抗（R）和運算放大器的噪聲。對于R=0，運算放大器噪聲電流源短路，整體輸入參考噪聲由運算放大器的電壓噪聲決定

 $1\frac{pA}{\sqrt{Hz}}$

當我們將源電阻增加到R=3kΩ和300kΩ時，運算放大器噪聲電流源預計會流過運算放大器的源阻抗和輸入阻抗。然而，由于運算放大器的輸入阻抗在幾個MΩ的范圍內，噪聲電流仍然主要通過源阻抗流動。因此，對于R=3kΩ和300kΩ，噪聲電流產生的等效噪聲電壓分別為

 $3\frac{nV}{\sqrt{Hz}}$ 和 300 $\frac{nV}{\sqrt{Hz}}$

對于R=3kΩ和300kΩ，運算放大器的噪聲電壓仍然會產生

 $3\frac{nV}{\sqrt{Hz}}$ 

因為這些電阻值與運算放大器輸入阻抗相比相對較小。

圖2中的表格還給出了所考慮的三個不同值的R熱噪聲。如圖所示，主要噪聲源（圖2中紅色矩形突出顯示）以及電路的整體噪聲性能隨源阻抗而變化。在使用噪聲系數度量時，這是一個需要記住的重要概念（稍后將討論）。

對替代噪聲度量的需求

輸入參考噪聲發生器模型不適合射頻設計。例如，在計算RF增益級的輸入參考噪聲電流時，我們需要測量該級在感興趣頻率下的跨阻抗。這種測量在高頻下非常具有挑戰性。因此，人們希望找到另一種在高頻下更容易測量的噪聲性能指標。

此外，在許多射頻系統中，我們對信號功率與噪聲功率的比值（信噪比或信噪比）感興趣。信噪比指定了信號的質量，并最終決定了我們的通信系統接收到的數字比特中有多少是錯誤的（系統的誤碼率）。

所需的信噪比取決于各種因素，例如：

調制方案

比特率

每比特能量

濾波器帶寬

大多數數字通信系統需要至少10dB的信噪比。在執行解調的接收器系統的輸出端測量信噪比。如圖3所示，典型的接收器信號鏈由幾個不同的塊組成，如低噪聲放大器（LNA）、混頻器、濾波器和模數轉換器（ADC）。

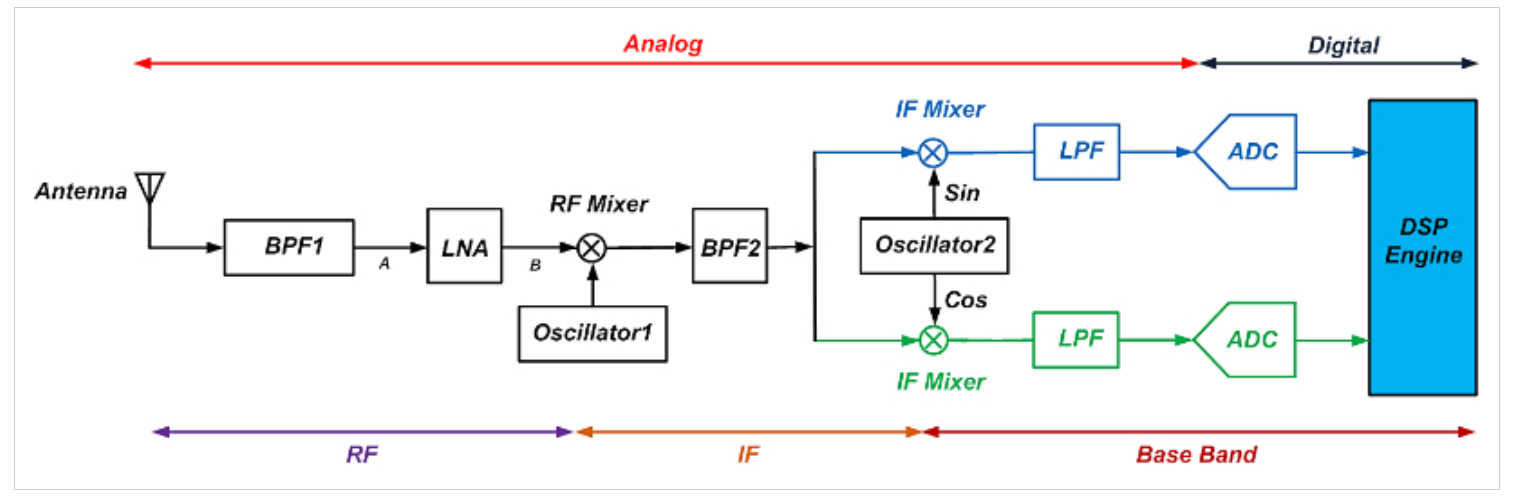
圖3。示例接收機信號鏈框圖。

射頻工程師需要知道這些電路組件中的每一個是如何影響噪聲性能的，以及信號在信號鏈中傳播時信噪比是如何降低的。因此，與信噪比直接相關的噪聲性能指標在射頻設計中可能更有幫助。這就是噪聲系數規范的突出之處，因為噪聲系數在高頻下更容易測量，并且直接基于信噪比規范定義。

噪聲系數和噪聲系數測量

電路的噪聲系數（F）定義為輸入端的信噪比與輸出端的信信噪比之比：

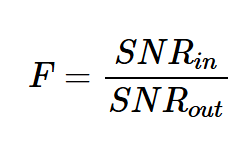
方程式1。

在上述方程中，噪聲和信號功率量以線性項表示，而不是以分貝表示。以分貝表示的噪聲系數稱為噪聲系數（NF）：

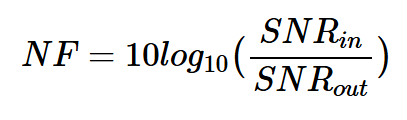
方程式2。

應當注意，一些參考文獻沒有做出這種區分，而是使用術語噪聲系數來指代方程1和2。在這種情況下，我們應該從上下文中確定噪聲系數是以分貝還是線性表示的。

對于無噪聲電路，輸入和輸出信噪比相同，導致F=1和NF=0 dB。噪聲系數是電路引起的信噪比劣化的直接度量。例如，如果電路輸入端的信噪比為60dB，電路噪聲系數為7dB，那么電路輸出端的信信噪比是53dB。更精確地說，假設電路的輸入噪聲功率等于計算電路NF的參考噪聲功率，則此陳述是有效的（我們將在即將發表的文章中對此進行詳細討論）。

其他噪聲系數定義

使用一點代數，我們可以從方程1中推導出有用的替代表達式。如果我們用Si和So表示電路輸入和輸出端的信號功率，用Ni和No表示輸入和輸出的噪聲功率，我們得到以下方程：

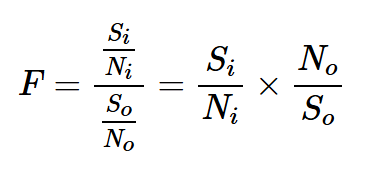
考慮到這一點，您可能會想知道，輸出信號與輸入信號有什么關系？由于這些是功率量，我們需要考慮電路的功率增益。在功率增益為G的情況下，我們得到So=GSi，這導致了方程3：

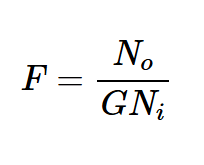
方程式3。

在方程式3中，No是輸出端的總噪聲。它包括電路內部噪聲源的影響以及源阻抗（或前一級的輸出阻抗）的噪聲。Ni是源阻抗（RS）在電路輸入端產生的噪聲。根據方程式3，噪聲因子是總輸出噪聲除以來自源電阻的輸出噪聲部分。

為了推導另一個表達式，讓我們關注源阻抗No（源）產生的輸出噪聲部分，以及電路內內部噪聲源No（添加）產生的部分。因此，我們得到：

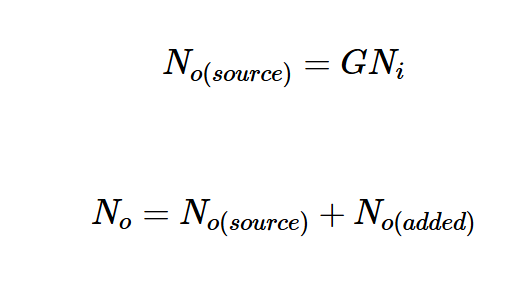
將這些方程代入方程3，得到方程4：

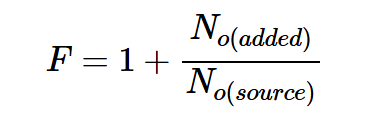
方程式4。

方程式4表明，我們獲得的噪聲系數值取決于連接到電路的源阻抗（RS）。在方程式4中，No（源）顯然是RS的函數。然而，根據我們在上一節中的討論，我們知道電路本身的噪聲也是RS的函數，因此，必須指定已知源阻抗的噪聲系數，通常為50Ω。

計算示例電路中的噪聲系數

在這個例子中，我們將使用方程式1和4來計算以下電路的噪聲系數（圖4）。

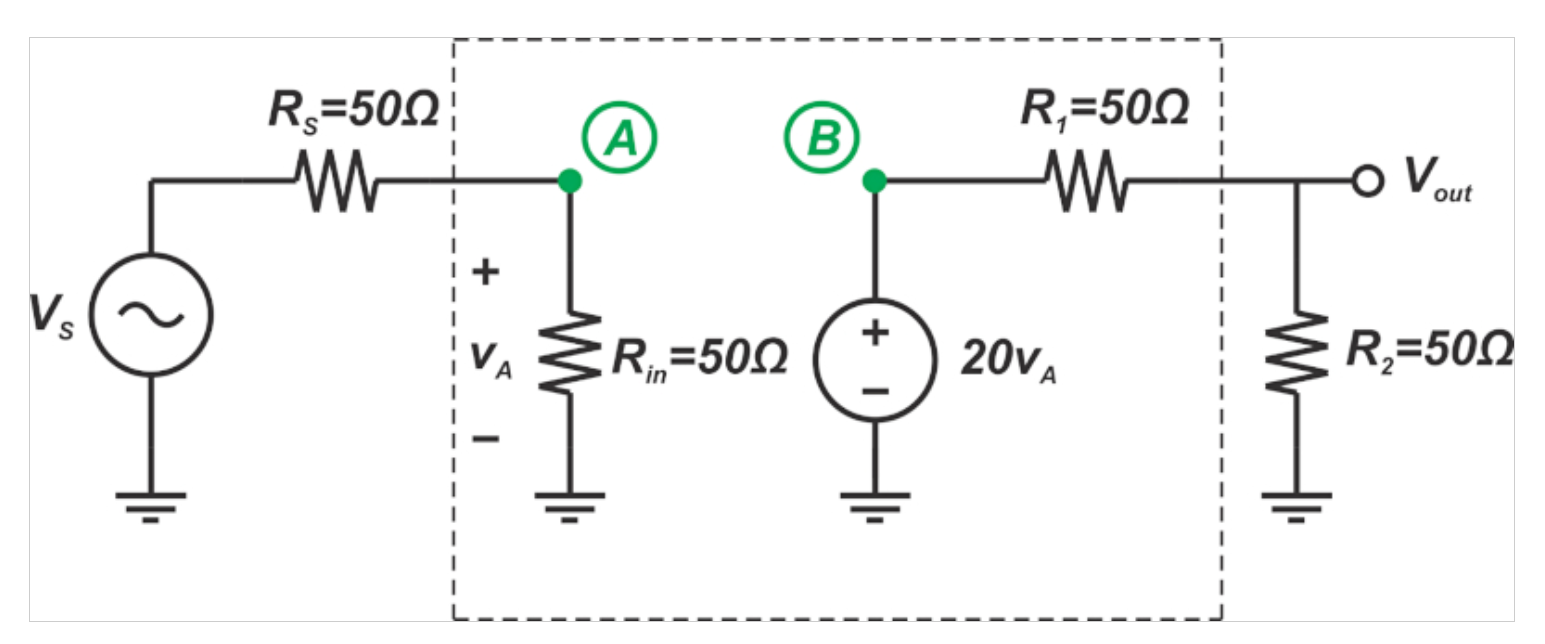
圖4。示例電路。

我們假設輸入電壓的均方根值為VS，所有電阻值均為50Ω，系統的噪聲帶寬為Bn=1 MHz。

為了使用方程1，我們需要計算電路輸入和輸出處的信噪比。由于RS=Rin，電路輸入端（節點A）的輸入信號減半。因此，節點A處信號的RMS值為：

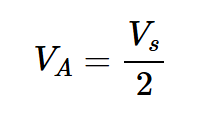
輸入信號功率為：

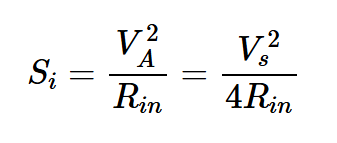
方程式5。

完成后，我們可能會問如何計算輸入噪聲。我們知道電阻R的均方根噪聲電壓

 $\mathrm{是V}/\sqrt{Hz}$ 

由以下公式給出：

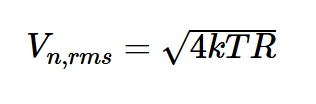
圖5顯示了計算RS噪聲的電路圖。

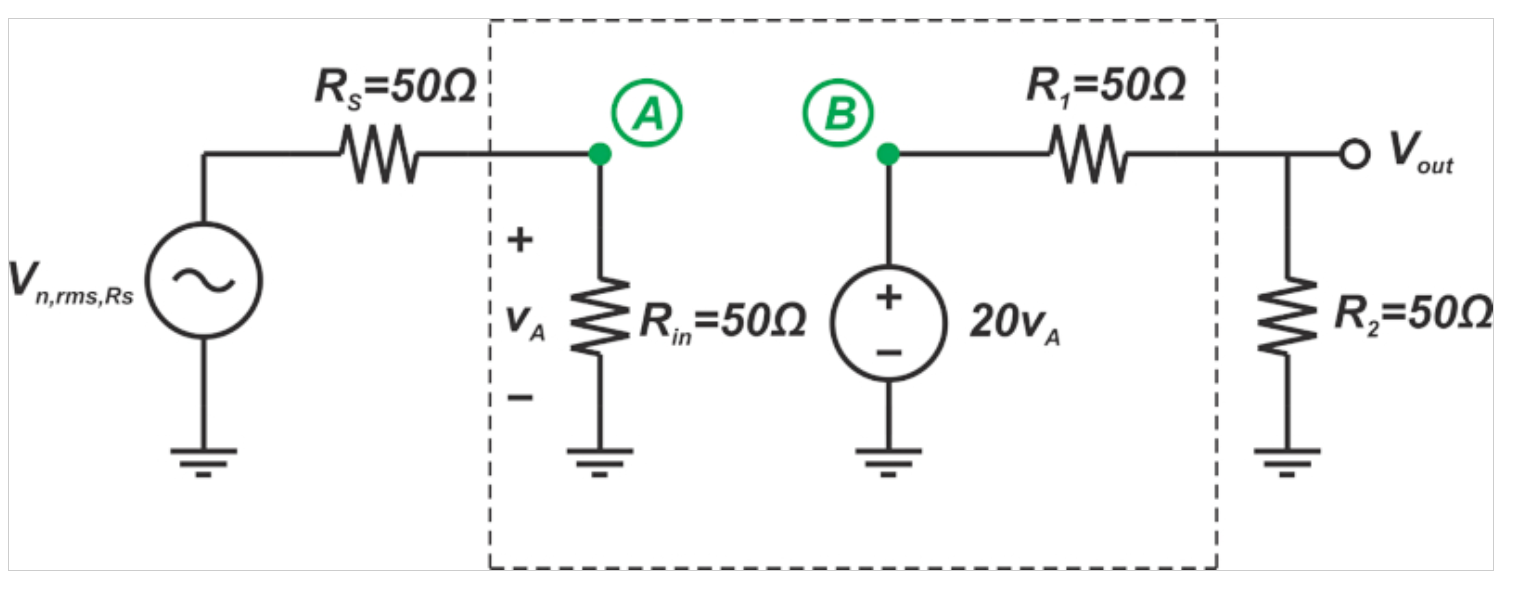
圖5。計算RS噪聲的示例電路圖。

在該圖中，輸入電壓源短路，RS的噪聲電壓與該電阻器串聯。由于RS=Rin，RS的噪聲電壓在輸入端減半，產生的輸入噪聲功率為：

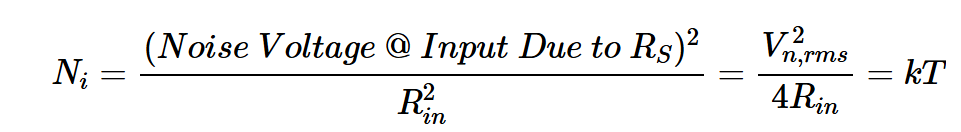
方程式6。

Ni是電路輸入端的噪聲功率。應當注意，Ni是在假設電路的輸入阻抗（Rin）無噪聲的情況下計算的。由于Vn，rms在

  $V/\sqrt{Hz}$,

，上述方程給出了每單位帶寬的噪聲功率$\left(V^2/Hz\right)$

因此，方程6的結果應乘以噪聲帶寬Bn，以找到感興趣帶寬上的總噪聲功率。考慮到帶寬，方程5和6給出了輸入信噪比：

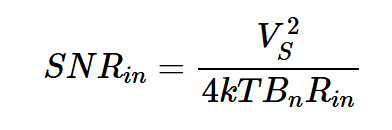
方程式7。

為了計算輸出信號和噪聲功率，我們需要找到電路的功率增益（輸出功率與輸入功率的比值）：

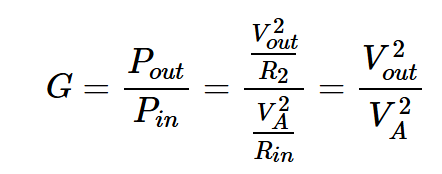
方程式8。

在上述方程中，Vout表示輸出電壓的RMS。從電路圖中，我們注意到：

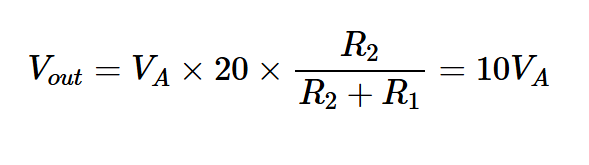
方程式8簡化為G=100。輸出信號功率計算如下：

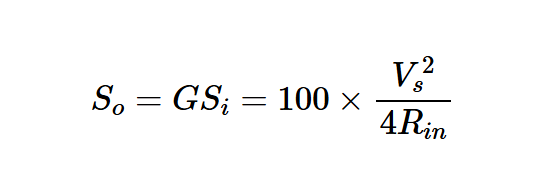
方程式9。

根據方程式6，源電阻引起的輸出噪聲計算如下：

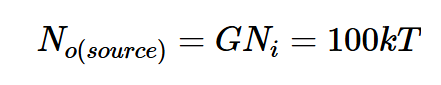
方程式10。

圖6顯示了計算Rin噪聲貢獻的電路圖。

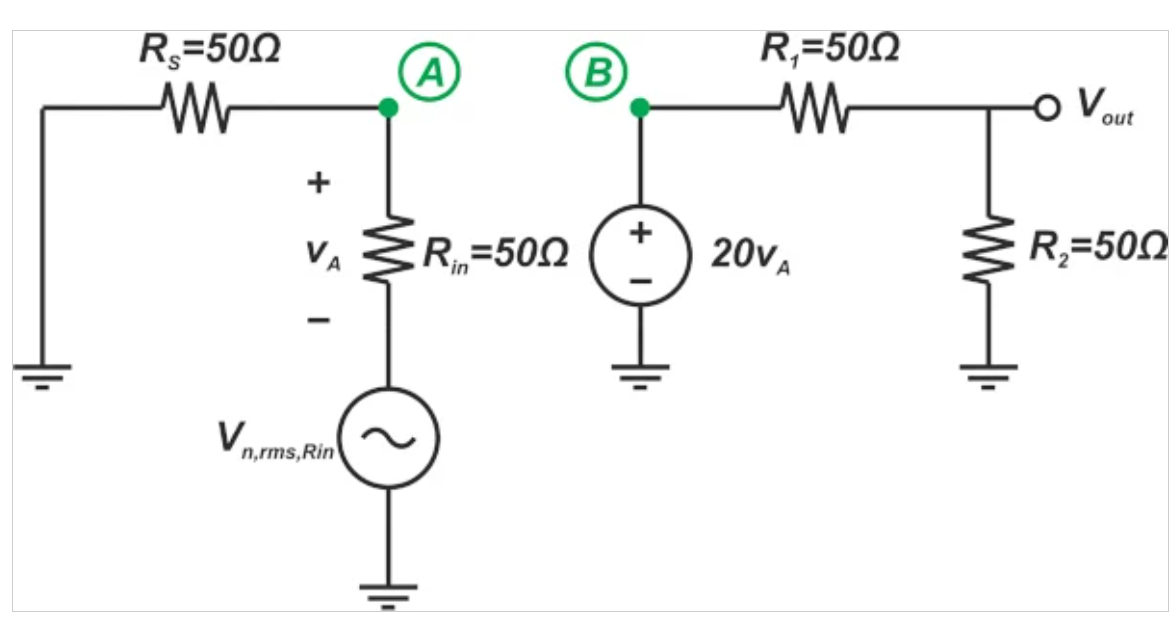
圖6。計算Rin噪聲貢獻的示例電路圖。

將上圖與圖5進行比較，我們可以得出結論，Rin的輸出噪聲與RS（100kT）的輸出噪聲相同。每個R1和R2的輸出噪聲功率可以很容易地計算為kT。因此，總輸出噪聲為：

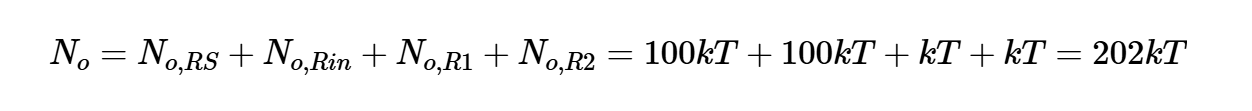
方程式11。

再次注意，方程式10和11給出了每單位帶寬的噪聲功率（V2/Hz），結果應乘以噪聲帶寬Bn，以找到感興趣帶寬上的總噪聲功率。方程式9和11給出了輸出信噪比：

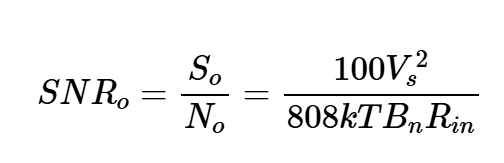
方程式12。

最后，根據方程式7和12，計算噪聲系數：

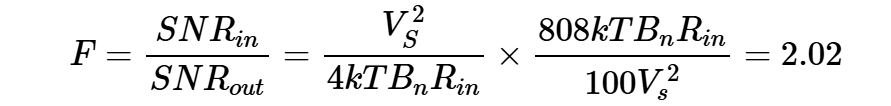
方程式13。

以分貝表示，我們得到NF=3.05dB。現在，讓我們使用方程4來分析電路噪聲系數。在這種情況下，我們只需要計算源阻抗No（source）產生的輸出噪聲部分和電路No（added）產生的部分。否（添加）可以根據方程式10和11計算：

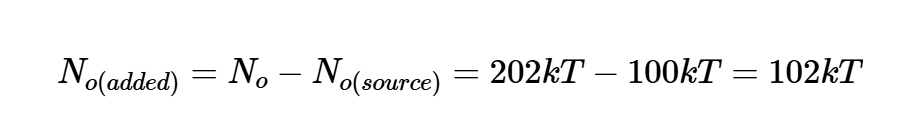
方程式14。

將方程10和14代入方程4，得到：

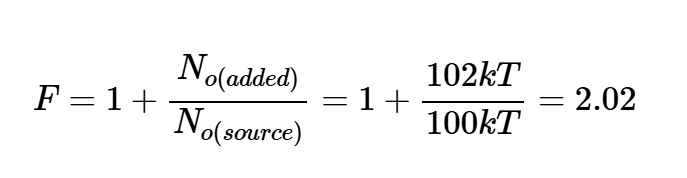
這與之前的計算結果一致。根據方程4，我們不需要計算輸入和輸出信號功率以及輸入和輸出信噪比。結果，可以更容易地計算方程4。