前面介紹了校正裝置的結構形式。為了滿足不同系統的控制性能要求,串聯校正裝置可設計成相位超前校正、相位遲后校正和和相位遲后-超前校正形式。本節首先介紹此三種裝置的無源和有源網絡結構,然后在此基礎上介紹頻率校正原理和MATLAB的設計方法。而關于串聯校正裝置的根軌跡方法則在下一節介紹。
6.2.1 超前校正
如前所述,為滿足控制系統的靜態性能要求,最直接的方法是增大控制系統的開環增益,但當增益增大到一定數值時,系統有可能變為不穩定,或即使能穩定,其動態性能一般也不會理想。為此,需在系統的前向通道中加一超前校正裝置,以實現在開環增益不變的前提下,系統的動態性能亦能滿足設計的要求。本節先討論超前校正網絡的特性,然后分別介紹基于頻率響應法的超前校正裝置的設計過程。 (一)超前校正裝置
圖6-3 超前校正裝置
(a) 無源校正裝置 (b)有源校正裝置 |
圖6-3分別為無源和有源超前校正網絡。對于無源校正裝置(a),忽略該網絡的輸入阻抗和輸出阻抗效應,則其傳遞函數為:
| 式中, | 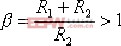 | ,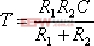 |
上式另一常見形式可寫作: | 式中, | 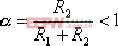 | ,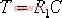 |
對于有源校正裝置(b),其對應的傳遞函數為:
| 式中, | 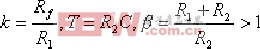 。 。 |
負號是因為采用了負反饋的運算放大器,再串聯一只反相運算放大器即可消除負號。 在式(6-3)中,令R1C=T1,R2C=T2 ,則(6-3)可寫成如下形式: 上式即為實際的比例微分控制器(PD)的傳遞函數的表達式。 超前校正裝置的零、極點分布如圖6-4所示,由于β>1 ,故 Gc(s)的零點總在其極點的右側。由式(6-1)和式(6-2)可知,在采用超前校正網絡時,系統的開環增益會有1/β (或k )倍的衰減。對此,用放大倍數β 或(1/k)的附加放大器予以補償。經補償后,令α=1/β ,其傳遞函數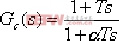 , ,
頻率特性為: 與式(6-5)對應的幅頻特性的表達式分別為: 其相應的極坐標如圖6-5。由圖可見,超前校正裝置的極坐標是一個位于第一象限的半圓,圓心坐標 [(1+1/α)/2,j0],半徑為 (1/α-1)/2,從坐標原點到半圓作切線,它與正實軸的夾角即為該校正裝置的最大超前角φm ,且有: 此最大超前角對應的頻率可由式(6-7)得到。令dφ(ω)/dω=0,則有:
對式(6-6)的幅頻特性取對數坐標,有:
根據式(6—7)、(6—10),可令 ,利用如下Matkab語句作出它的伯德圖,如圖6—6所示。 alpha=0.1; T=1; Gc=tf([T,1],[alpha*T,1]); [x0,y0,w]=Bode(Gc);[x,y]=bode_asymp(Gc,w); subplot(211),semilogx(w,20*log10(x0(:)),x,y) subplot(212),semilogx(w,y0(:))
由式(6—7)可知,由于α1,因而當 0ω∞時,校正網絡的相位總是正值。這明輸出信號在相位上總超前于輸入信號一個角度,因而稱該校正網絡為超前校正。同時,由于當ω→0,L(ω)→0 ;當ω→+∞時,L(ω)→最大值20lg(1/α) ,所以超前校正裝置又是一個高通濾波器。
比較圖6-4和圖6-5可見,ωm是Gc(s)零點和極點的幾何平均值。理論上,最大相位超前角φm不大于90°,但實際上,一般超前校正網絡的最大相位超前角φm不大于65° 。如果要得到大于65°的相位超前角,可用兩個超前校正網絡相串聯來實現,并在串聯的兩個網絡之間加一隔離放大器,以消除它們之間的負載效應。 6.2.2 遲后校正
與超前校正相反,如果一個控制系統具有良好的動態性能,但其靜態性能指標較差(如靜態誤差較大)時,則一般可采用遲后校正裝置,使系統的開環增益有較大幅度的增加,而同時又可使校正后的系統動態指標保持原系統的良好狀態。 (一) 遲后校正裝置
無源的遲后校正裝置可由圖6—7(a)構成。由圖可得到該校正裝置的傳遞函數 | 式中, | 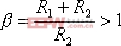 | ,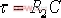 |
有源的遲后校正裝置由圖6-7(b)構成。其傳遞函數為: 式中, Ti=R2C,k=R2/R1,同樣等式右邊的負號可通過串聯一反相器加以抵消,因而(6-12)可改寫為比例積分控制器PI的形式: (二)遲后校正裝置的極點及頻率特性
由式(6-11)可分別得到該遲后校正裝置的零、極點分布圖(6—8)、極坐標圖(6—9)、伯德圖(6—10) | 圖中, | 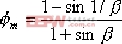 | , |
比較超前校正裝置和遲后校正裝置可以發現,遲后校正裝置具有如下特點: 1)輸出相位總滯后于輸入相位,這是校正中必須要避免的; 2)它是一個低通濾波器,具有高頻率衰減的作用; 3)利用它的高頻衰減作用(當 ),使校正后系統剪切頻率 前移,從而達到增大相位裕量的目的。 6.2.3 遲后-超前校正
(一) 遲后-超前校正裝置 上圖構成了遲后-超前的無源和有源裝置,無源校正裝置的傳遞函數為:
上式中,令:T1=R1C1,T2=R2C2,T1/β+βT2=R1C1+R2C2+R1C2,β>1,且令 T2>T1。同時,上式也可改寫成如下形式:
其中前半部分起超前作用,后半部分起遲后作用。 同理,有源校正裝置的傳遞函數為:
顯然,有源遲后-超前校正裝置的傳遞函數同時是一個典型的PID控制器,式中:KP為比例系數,Ti 積分時間常數,Td為微分時間常數。 (二)遲后-超前校正裝置的極點及頻率特性
根據遲后-超前裝置的傳遞函數,可得到其頻率特性: 其對應的幅頻特性和相頻特性分別為:
根據上面二式可分別畫出其零、極點分布圖、極坐標圖、伯德圖。從圖中看出,因 T2>T1,遲后部分的零極點更靠近原點,使系統的靜態性能得到改善。 從圖6-13和6-14可以看出當ω從0→ω1 變化時,遲后-超前校正裝置起超前作用,而當ω從ω1→∞ 變化時,校正裝置起遲后作用。由下列Matlab語句可得到其伯德圖: alpha=[0.1:0.1:0.5]; T1=1;T2=5; Gc=tf([T1,1],[alpha*T1,1])*tf([alpha*T2,i],[T2,1]); [x0,y0,w]=bode(Gc);[x,y]=bode_asymp(Gc,w); subplot(211),semilogx(w,20*log10(x0(:)),x,y) subplot(212),semilogx(w,y0(:)) 同時,容易計算相角為零的頻率ω1 為: 可見,遲后-超前校正裝置是超前裝置和遲后裝置的組合。 |
評論