為了使控制系統能可靠地工作,不但要求它能穩定,而且還希望有足夠的穩定裕量,使系統在環境發生變化或存在干擾的情況下仍能工作,這即為相對穩定性的概念。 在討論系統的穩定裕量時,首先要假定開環系統是穩定的,是最小相位系統,即開環系統的零、極點均僅位于s的左半平面,否則討論系統的穩定裕量是無意義的。
為了說明相對穩定性的概念,圖5-49為一典型的I型系統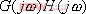 曲線,其開環系統的傳遞函數為: 曲線,其開環系統的傳遞函數為: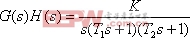 。根據奈氏判據可知,當 。根據奈氏判據可知,當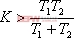 時,系統不穩定,奈氏曲線包圍(-1,j0)點;當 時,系統不穩定,奈氏曲線包圍(-1,j0)點;當 時,系統產生等幅振蕩,奈氏曲線經過(-1,j0)點;當 時,系統產生等幅振蕩,奈氏曲線經過(-1,j0)點;當 時,系統穩定,奈氏曲線不包圍(-1,j0)點。因此直觀地看,對于開環穩定的系統,要求閉環系統有一定的穩定性,不僅要求 時,系統穩定,奈氏曲線不包圍(-1,j0)點。因此直觀地看,對于開環穩定的系統,要求閉環系統有一定的穩定性,不僅要求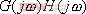 的幅頻特性不包圍(-1,j0)點,而且應與該點有一定的距離,即有一定的穩定裕量。 的幅頻特性不包圍(-1,j0)點,而且應與該點有一定的距離,即有一定的穩定裕量。 衡量閉環系統相對穩定性的具體指標有幅值裕量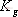 和相位裕量 和相位裕量 。在Matlab中,相應地有專門的函數來求取上述指標:Margin。具體用法參見下面的例子。 。在Matlab中,相應地有專門的函數來求取上述指標:Margin。具體用法參見下面的例子。 5.5.1 用奈氏圖表示相位裕量和幅值裕量
1、 相位裕量 設一開環穩定的系統的奈氏曲線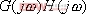 負實軸相交于G點,與單位圓相交于C點,如圖5-50。對應于 負實軸相交于G點,與單位圓相交于C點,如圖5-50。對應于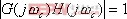 時的頻率 時的頻率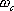 (交點C)稱為增益穿越頻率,又稱剪切頻率或交界頻率。在剪切頻率 (交點C)稱為增益穿越頻率,又稱剪切頻率或交界頻率。在剪切頻率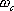 處,使系統達到臨界穩定狀態時所能接受的附加相位遲后角,定義為相位裕量,用 處,使系統達到臨界穩定狀態時所能接受的附加相位遲后角,定義為相位裕量,用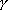 表示之。對于任何系統,相位裕量 表示之。對于任何系統,相位裕量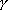 的算式為 的算式為 式中,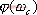 是開環頻率特性在剪切頻率 是開環頻率特性在剪切頻率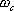 處的相位。 處的相位。 不難理解,對于開環穩定的系統,若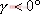 ,表示 ,表示 曲線包圍(-1,j0)點,相應的閉環系統是不穩定的;反之,若 曲線包圍(-1,j0)點,相應的閉環系統是不穩定的;反之,若 ,則相應的閉環系統是穩定的。一般 ,則相應的閉環系統是穩定的。一般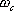 越大,系統的相對穩定性也就越好。因為系統的參數并非絕對不變,如果 越大,系統的相對穩定性也就越好。因為系統的參數并非絕對不變,如果 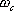 太小,就有可能因參數的變化而使奈奎斯特曲線包圍(-1,j0)點,即導致系統不穩定。 太小,就有可能因參數的變化而使奈奎斯特曲線包圍(-1,j0)點,即導致系統不穩定。 2、 幅值裕量 幅值裕量是系統相對穩定性的另一度量指標。如圖5-50所示,開環頻率特性的相角 時的頻率 時的頻率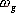 (交點G)處, (交點G)處,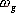 稱為相位穿越頻率,又稱為相位交界頻率。開環幅值 稱為相位穿越頻率,又稱為相位交界頻率。開環幅值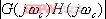 的倒數稱為增益裕量,用 的倒數稱為增益裕量,用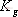 表示。即 表示。即 上式表示系統在變到臨界穩定時,系統的增益能增大多少。 由奈奎斯特穩定判據可知,對于最小相位系統,其閉環穩定的充要條件是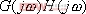 曲線不包圍(-1,j0)點,即 曲線不包圍(-1,j0)點,即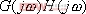 曲線與其負實軸交點處的模小于1,此時對應的 曲線與其負實軸交點處的模小于1,此時對應的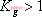 。反之,對于不穩定的系統,其 。反之,對于不穩定的系統,其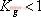 ,如圖5-51所示,閉環系統是不穩定的。 ,如圖5-51所示,閉環系統是不穩定的。 5.5.2 用伯德圖表示相位裕量和幅值裕量
上述的相位裕量和幅值裕量也可在對數幅相圖(Bode圖)上表示。對應于圖5-5
技術專區
主站蜘蛛池模板:
威远县|
平顺县|
五大连池市|
珲春市|
乐山市|
永和县|
天水市|
深水埗区|
准格尔旗|
芷江|
白河县|
抚松县|
抚州市|
哈巴河县|
米易县|
酉阳|
杭锦后旗|
漳州市|
化州市|
灵川县|
余江县|
尼玛县|
德昌县|
灵武市|
青海省|
丹寨县|
夏河县|
临武县|
淮安市|
巴林左旗|
万安县|
遂昌县|
临漳县|
罗江县|
铜山县|
荣成市|
贵定县|
定兴县|
洛南县|
彰武县|
侯马市|
|
評論