頻率響應法是通過系統的開環頻率特性和閉環頻率特性的一些特征量間接地表征系統瞬態響應的性能,因而這些特征量又被稱為頻域性能指標。常用的頻域性能指標包括:開環頻率特中的相位裕量、增益裕量;閉環頻率特中的諧振峰值、頻帶寬度和諧振頻率等。在時域分析中,控制系統包括靜態性能指標和動態性能指標。雖然這些頻域性能指標沒有時域性能指標那樣直觀,但對于二階系統而言,它們與時域性能指標間有著確定的對應關系;在高階系統中,只要存在一對閉環主導極點,則它們也有著近似的對應關系。
5.6.1 開環頻率特性中相位裕量與時域性能指標的關系 關于開環頻率特性低頻段與閉環系統靜態性能的關系我們在5.3.4中已作了分析,此處我們著重研究二階系統的相位裕量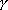 、剪切頻率 、剪切頻率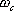 與阻尼比 與阻尼比 間的關系。 間的關系。 當 時, 時,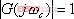 ,即 ,即 求解上式,得 據此求得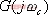 的相角為 的相角為 由相位裕量的定義得 圖5-59為 與 與 的關系曲線。 的關系曲線。 1、 與超調量的關系 在前面第三章已知,超調量 和阻尼比 之間的定量關系為 將式(5-62)和式(5-63)的函數關系,以 為橫坐標, 為橫坐標,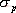 和 和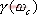 為縱坐標,繪制于同一張圖上,如圖5-60所示。這樣,根據給定的相位裕量 為縱坐標,繪制于同一張圖上,如圖5-60所示。這樣,根據給定的相位裕量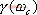 就可由圖5-60直接得到時域特性的最大超調量 就可由圖5-60直接得到時域特性的最大超調量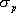 。反之,當要求超調量不超過某一允許的 。反之,當要求超調量不超過某一允許的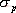 值時,也可以從圖5-60中求得應有的相信裕量 值時,也可以從圖5-60中求得應有的相信裕量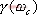 。 。
圖5-60 二階系統相位裕量、最大超調量與阻尼比關系
|
2、 與調整時間的關系 相位裕量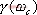 與調整時間 與調整時間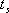 之間的定量關系。仍以二階系統為例,在第三章已求得調整時間 之間的定量關系。仍以二階系統為例,在第三章已求得調整時間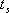 的近似表達式 的近似表達式 將式(5-60)代入式(5-64)可得 再由式(5-62)和式(5-65)可得 將式(5-66)的函數關系繪成曲線,如圖5-61所示(圖中畫的是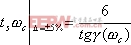 的關系式)。 的關系式)。 如果有兩個系統,其相位裕量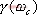 相同,那么他們的最大超調量 相同,那么他們的最大超調量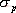 (時域)是大致相同的,但他們的調整時間 (時域)是大致相同的,但他們的調整時間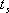 并不一定相同。由式(5-66)可知, 并不一定相同。由式(5-66)可知,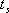 與剪切頻率 與剪切頻率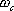 成反比,即 成反比,即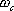 越大,時域的調整時間 越大,時域的調整時間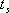 越短。所以剪切頻率 越短。所以剪切頻率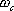 在頻率特性中是一個很特殊的重要參數,它不僅影響系統的相位裕量,還影響動態過程的調整時間 在頻率特性中是一個很特殊的重要參數,它不僅影響系統的相位裕量,還影響動態過程的調整時間
上述的頻域性能與時域性能的定量關系都是基于二階系統得出來的。對于高階系統,只要存在一對閉環主導極點,就可以利用上述二階系統分析的一些定量關系,以簡化系統的設計 5.6.2 閉環頻率特性及其特征量 由于開環和閉環頻率特性間有著確定的關系,因而可以通過開環頻率特性求取系統的閉環頻率特性。對于單位反饋系統,其閉環傳遞函數為 對應的閉環頻率特性為 上式描述了開環頻率特性與閉環頻率特性之間的關系。如果已知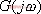 曲線上的一點,就可由式(5-67)確定閉環頻率特性曲線上相應的一點。 曲線上的一點,就可由式(5-67)確定閉環頻率特性曲線上相應的一點。 對于非單位反饋系統,如圖5-62a,則可先將其等效為如圖5-62b的系統,然后按上法先求圖5-62b中單位反饋系統的頻率特性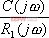 ,再與頻率特性 ,再與頻率特性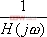 相乘,即可得到總的閉環頻率特性。 相乘,即可得到總的閉環頻率特性。 用這種方法逐點繪制閉環頻率特性曲線,在工程上,常用等M圓、等N圓和Nicoles圖線來表示閉環系統的頻率特性,并用用圖解法去繪制。顯然這是既繁瑣又費時間的工作。現在這些工作可由計算機軟件實現,例如在Matlab中就有專門的繪制等M圓、等N圓和Nicoles圖線的函數,從而大大提高了繪圖的效率和精度。本節我們不對閉環頻率特性的繪制方法進行研究,僅對閉環頻率特性與時間性能指標間的關系作些分析。 1. 閉環頻率特性的諧振峰值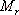 與諧振頻率 與諧振頻率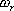 在本章第三節,針對二階系統我們給出了二階振蕩環節的諧振峰值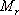 和諧振頻率 和諧振頻率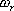 的概念,閉環系統的幅值在諧振頻率 的概念,閉環系統的幅值在諧振頻率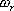 處所取得的最大值 處所取得的最大值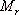 ,稱為諧振峰值。如圖5-63所示。 ,稱為諧振峰值。如圖5-63所示。 2. 截止頻率和頻帶寬度 圖5-63為 時閉環對數幅頻特性的一般形狀。當幅頻值下降到低于零頻率值以下3dB時,對應的頻率 時閉環對數幅頻特性的一般形狀。當幅頻值下降到低于零頻率值以下3dB時,對應的頻率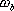 稱為截止頻率,即有 稱為截止頻率,即有 對應于閉環幅頻值不低于-3dB的頻率范圍 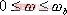 ,通常稱為系統的頻帶寬度。系統的頻帶寬度反映了系統復現輸入信號的能力,具有寬的帶寬的系統,其瞬態響應的速度快,調整的時間也小。 ,通常稱為系統的頻帶寬度。系統的頻帶寬度反映了系統復現輸入信號的能力,具有寬的帶寬的系統,其瞬態響應的速度快,調整的時間也小。 例5-11 試比較兩個系統帶寬的大小,并驗證... 設有二個控制系統,它們的傳遞函數分別為 系統I: 系統Ⅱ: 試比較兩個系統帶寬的大小,并驗證具有較大帶寬的系統比具有較小帶寬的系統響應速度快,對輸入信號的跟隨性能好。 解 圖5-64a為上述兩系統的閉環對數幅頻特性曲線(圖中虛線為其漸近線)。由圖可見,系統I的帶寬為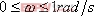 ,系統Ⅱ的帶寬為 ,系統Ⅱ的帶寬為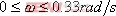 ,即系統I的帶寬是系統Ⅱ帶寬的三倍。圖5-64b表示了兩系統的階躍響應曲線。顯然,系統I較系統Ⅱ具有較快的階躍響應,并且前者跟蹤階躍輸入的性能也明顯優于后者。 ,即系統I的帶寬是系統Ⅱ帶寬的三倍。圖5-64b表示了兩系統的階躍響應曲線。顯然,系統I較系統Ⅱ具有較快的階躍響應,并且前者跟蹤階躍輸入的性能也明顯優于后者。 需要指出,寬的帶寬雖然能提高系統響應的速度,但也不能過大,否則會降低系統過濾高頻噪聲的能力。因此在設計系統時,對于頻帶寬度的確定必須兼顧系統的響應速度和抗高頻干擾的要求,采取一種折衷的方案。
5.6.3 閉環頻域特性與時域響應性能指標的關系
對于二階系統,其時域響應與頻域響應之間有著確定的對應關系。標準二階系統對應的閉環頻率特性為 式中 當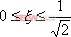 時,系統有諧振產生,由本章第三節討論可知,其諧振峰值分別為 時,系統有諧振產生,由本章第三節討論可知,其諧振峰值分別為 由式(5-70)得 1、諧振峰值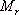 和最大超調量 和最大超調量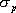 的關系 的關系 為了便于對諧振峰值 和最大超調量 和最大超調量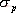 作比較,把 作比較,把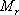 和 和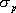 與 與 的關系曲線都畫在圖5-65中。由圖可見, 的關系曲線都畫在圖5-65中。由圖可見,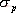 和 和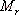 均隨著 均隨著 的減小而增大。顯然,對于同一個系統,若在時域內的 的減小而增大。顯然,對于同一個系統,若在時域內的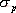 大,則在頻域中的 大,則在頻域中的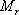 必然也是大的;反之亦然。為了使系統具有良好的相對穩定性,在設計系統時,通常取 必然也是大的;反之亦然。為了使系統具有良好的相對穩定性,在設計系統時,通常取 值在 值在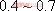 之間,對應的 之間,對應的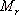 將坐落在 將坐落在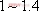 之間。 之間。 把式(5-70)代入式(5-63),則得 如果已知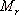 ,則由上式可求得對應的 ,則由上式可求得對應的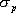 。 。 2、諧振峰值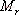 和調整時間 和調整時間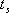 、峰值時間 、峰值時間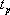 關系 關系 根據在第三章中導出二階系統的上升時間和調整時間的關系式,并考慮到式(5-69),則得 由式(5-70)有: 將式(5-75)的函數關系用曲線表示,如圖5-66。可見,峰值時間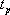 與諧振峰值 與諧振峰值 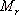 成正比,而峰值時間 成正比,而峰值時間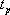 與諧振頻率 與諧振頻率 成反比。調整時間 成反比。調整時間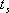 與 與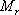 和 和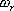 的關系和峰值時間 的關系和峰值時間 與它們的關系相同。同時上述兩式表明,如果已知 與它們的關系相同。同時上述兩式表明,如果已知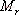 和 和 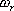 ,就能從上述關系式中求出 ,就能從上述關系式中求出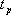 和 和 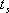 。 。 3、頻帶寬度與峰值時間、調整時間的關系 根據頻帶寬度的定義,當 時,二階系統的幅頻為 時,二階系統的幅頻為 求解上式,得 同理,注意到式(5-73)、(5-74),并對照式(5-69),則得 由式(5-78)和(5-79)可知,對于給定的 , , 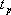 和 和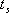 均與 均與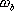 成反比。這就是說, 成反比。這就是說,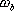 越大,則系統響應的速度就越快。 越大,則系統響應的速度就越快。 把式(5-70)代入式(5-78)、(5-79),可求得 上述兩式把時域性能指標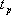 、 、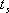 與頻域性能指標 與頻域性能指標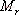 和 和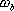 聯系起來,如果已知 聯系起來,如果已知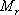 和 和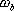 ,就能從上述關系式中求出 ,就能從上述關系式中求出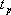 和 和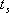 。 。 對于高階系統,系統的頻率響應與時域響應間的對應關系可通過經驗公式聯系,也通過傅氏積分,即, 由于這種積分變換較復雜,因而不可能像二階系統那樣簡單地描述頻域響應與時域響應間的對應關系,其積分一般借助于計算機輔助算法,且目前這些算法均比較成熟。如果高階系統中有一對共軛主導極點,則上述二階系統的時域響應與頻域響應間的對應關系就可近似地應用于高階系統中去。 |
評論