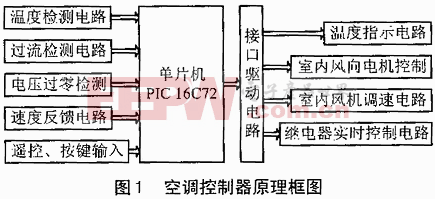
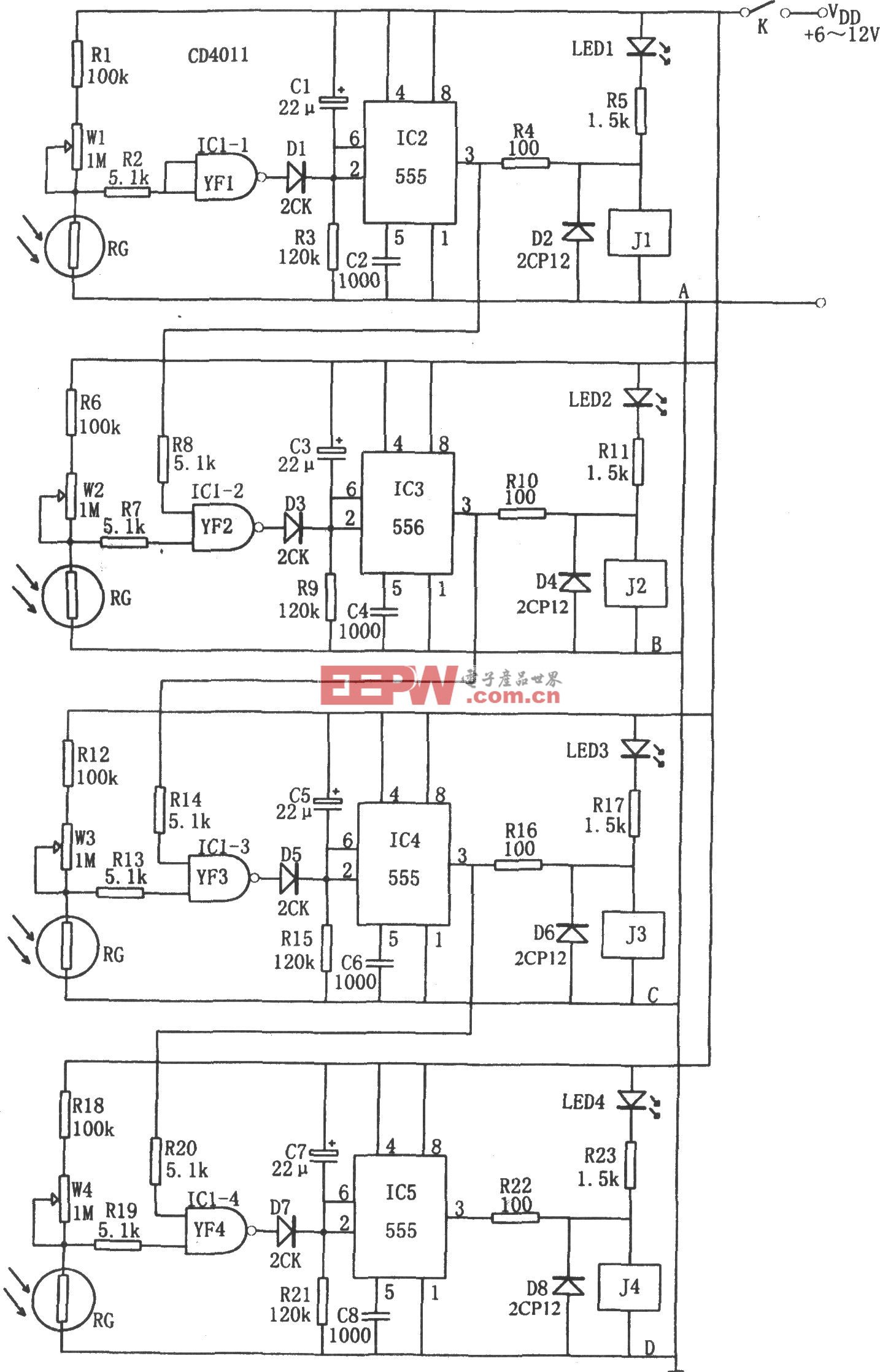
控制系統(tǒng)的時域分析法--控制系統(tǒng)的穩(wěn)態(tài)誤差

務請注意，使用拉普拉斯變換終值定理計算穩(wěn)態(tài)誤差終值的條件是：sEr(s)在s平面右半部及虛軸上除了坐標原點是孤立奇點外必需解析，亦即sEr(s)的全部極點除坐標原點外應全部分布在s平面的左半部。例如給定輸入為正弦函數(shù)時

其象函數(shù)

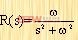在s平面的全部虛軸上不解析，就不能使用終值定理去求取系統(tǒng)的穩(wěn)態(tài)誤差終值。

3.2.4 動態(tài)誤差

靜態(tài)誤差系數(shù)的一個明顯特點，是對于一個給定系統(tǒng)只有一個系數(shù)呈現(xiàn)有限值，其它的系數(shù)不是零就是無窮大。因而，通過靜態(tài)誤差系數(shù)求得的靜態(tài)誤差或是零，或是有限的非零值，或是無窮大。所以，誤差隨時間的變化規(guī)律不能運用這種系數(shù)求出。但有些時候人們關心的往往是誤差隨時間變化的情況，這種誤差表現(xiàn)了誤差隨時間變化的規(guī)律，稱之為動態(tài)誤差。本節(jié)介紹的動態(tài)誤差將提供一些關于誤差怎樣隨時間變化的信息，即，系統(tǒng)在給定的輸入作用下穩(wěn)態(tài)誤差是否會與t，t2等成比例地增加。

動態(tài)誤差不同但穩(wěn)態(tài)誤差系數(shù)相同的系統(tǒng) 首先論證兩個具有不同動態(tài)誤差的系統(tǒng)卻能夠有相同的靜態(tài)誤差系數(shù)。設以下的兩個系統(tǒng)：

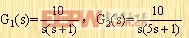其靜態(tài)誤差系數(shù)由下列各式給出:
Kp1=∞， Kp2=∞
Kv1=10， Kv2=10
Ka1=0， Ka2=0

于是，對于同樣的階躍輸入，兩個系統(tǒng)有相同的穩(wěn)態(tài)誤差。當然，對于斜坡和拋物線輸入的穩(wěn)態(tài)誤差，該結論也同樣適用。這個分析表明，不能根據(jù)靜態(tài)誤差系數(shù)去估算系統(tǒng)的動態(tài)誤差。

動態(tài)誤差系數(shù) 現(xiàn)在引進動態(tài)誤差系數(shù)來描述動態(tài)誤差。通過用E(s)/R(s)的分母多項式除它的分子多項式的方法，把E(s)/R(s)展開成下列s的升冪級數(shù)：

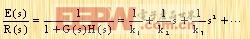冪級數(shù)的系數(shù)K1、K2、K3、…被定義為動態(tài)誤差系數(shù)。對N型系統(tǒng)的動態(tài)誤差系數(shù)由下式給出：

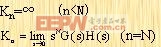其中
K1=動態(tài)位置誤差系數(shù)；
K2=動態(tài)速度誤差系數(shù)；
K3=動態(tài)加速度誤差系數(shù)。

需要說明的是，在一個給定系統(tǒng)中，動態(tài)誤差系數(shù)是與靜態(tài)誤差系數(shù)有關的。例如：設下列具有單位反饋的0型系統(tǒng)：

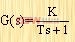其靜態(tài)位置誤差系數(shù)、靜態(tài)速度誤差系數(shù)和靜態(tài)加速度誤差系數(shù)分別是

其中
Kp=K
Kv=0
Ka=0

由于E(s)/R(s)可展開成

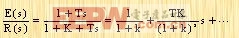所以，依據(jù)靜態(tài)誤差系數(shù)給出的動態(tài)誤差系數(shù)如下：
k1=1+K=1+Kp

動態(tài)速度誤差系數(shù)由下式給出：

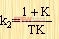當E(s)寫成下面的形式時：
E(s)= R(s)+ sR(s)+ s2R(s)+…

動態(tài)誤差系數(shù)的優(yōu)點就更為清楚。這個級數(shù)的收斂域是s=0的鄰域，這相當于在時域內的t=∞。假定所有的初始條件為零，并且忽略掉在t=0的鄰域，這相當于在時域內的t=∞。假定所有的初始條件為零，并且忽略掉在t=0時的脈沖，則對應的時間解（即穩(wěn)態(tài)誤差）由下式求出：

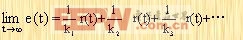這樣，由輸入函數(shù)和它的導數(shù)所引起的穩(wěn)態(tài)誤差能根據(jù)動態(tài)誤差系數(shù)求出，這便是動態(tài)誤差系數(shù)的一個優(yōu)點。

如果E(s)/R(s)圍繞原點展開成一個冪級數(shù)，級數(shù)的逐項系數(shù)就表示系統(tǒng)在緩慢變化的輸入作用下的動態(tài)誤差。動態(tài)誤差系數(shù)是計算任意輸入作用下的誤差信號和穩(wěn)態(tài)誤差的簡便方法。用這個方法就不需要實際去解系統(tǒng)的微分方程。

例3-9

設前向傳遞函數(shù)為G(s)= 的單位反饋控制系統(tǒng)，求出它的動態(tài)誤差系數(shù)。還要求出當輸入量為r(t)=a0+a1t+a2t2時的穩(wěn)態(tài)誤差。

對于該系統(tǒng) = =0.1s+0.09s2-0.019s3+…

即 =0.1 (t)+0.09 (t)-0.019 (t)+…

則動態(tài)誤差系數(shù)是 k1=∞

k2=1/0.1=10

k3=1/0.09=11.1

由于r(t)由下式給出：r(t)=a0+a1t+a2t²

得(t)=a1+a2t，(t)=2a2，(t)=0

于是，穩(wěn)態(tài)誤差為

= [0.1(a1+a2t)+0.09(2a2)]= (0.1a1+0.18a2+0.2a2t)

只要不是a2=0，穩(wěn)態(tài)誤差就變?yōu)闊o窮大。

由以上分析可知，如果E(s)/R(s)圍繞原點展開成一個冪級數(shù)，級數(shù)的逐項系數(shù)就表示系統(tǒng)在緩慢變化的輸入作用下的動態(tài)誤差。動態(tài)誤差系數(shù)是計算任意輸入作用下的誤差信號和穩(wěn)態(tài)誤差的簡便方法。用這個方法就不需要實際去解系統(tǒng)的微分方程。