一文講透一階系統的系統響應、傳遞函數和輸出響應
一:一階系統響應定義
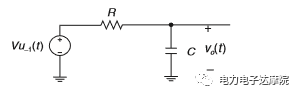
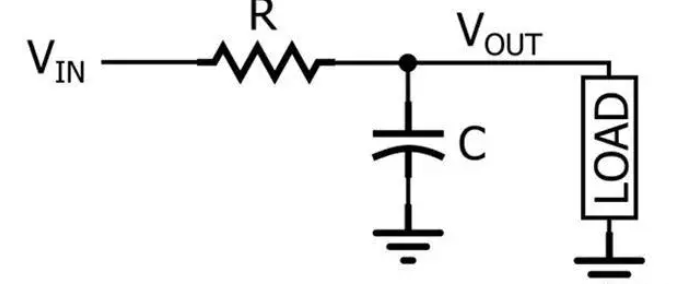
本文引用地址:http://www.104case.com/article/201901/396516.htm通常來講,一階系統分為電壓驅動一階系統(a)以及電流驅動一階系統(b),如下圖所示:
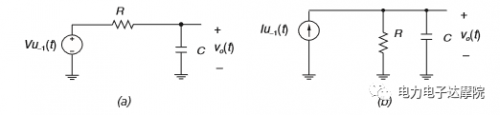
這兩個一階系統在線路上是完全等效的。它們的階躍響應如下:

電壓或者電流的上升時間在這里定義為從10%開始,上升到90%結束所需要的時間。對于一階系統,可以推導出上升時間為:
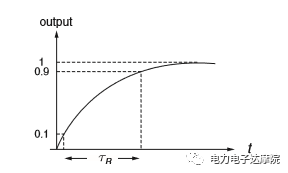
帶寬定義為AC輸入信號激勵下輸出響應幅值降到直流信號幅值的70.7%(或-3dB)所對應的頻率。
一階系統的傳遞函數表達式如下:
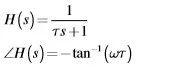
由此可以推導出一階系統的帶寬為:
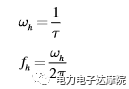
由以上數學表達式,我們很容易得出一階系統的上升時間與帶寬的關系為:
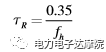
由此可知,一階系統的上升時間與帶寬成反比,這也就是為什么我們經常說帶寬變寬,系統響應速度會變快的理論解釋。
二:一階系統在低頻和高頻下的近似響應
從一階系統的傳遞函數,我們知道一階系統的幅值,相角以及群延時的表達式如下:
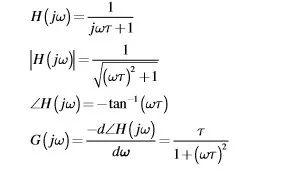
其中群延時是表征系統中頻率信號所經歷的延時時間。
一階系統只有一個極點,接下來我們看看此一階系統在低頻和高頻下的行為是怎么樣的,低頻或者高頻都是相對極點頻率所言。對于高頻,我們假定wτ?1,此時一階系統的幅值、相角以及群延時近似為:

因此,對于高頻一階系統,傳遞函數的幅值近似以20dB/十倍頻的速度衰減,相移近似為-90度,群延時隨著頻率的平方減少,頻率高的信號比頻率低的信號群延時要少。
對于低頻信號,即wτ?1,我們可以近似得到如下傳函:
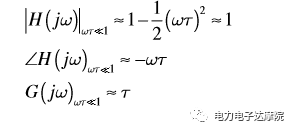
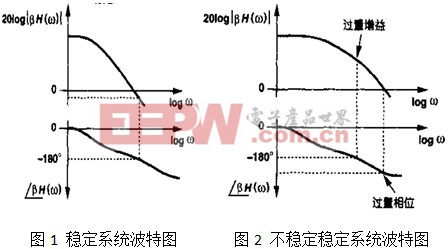
因此,對于低頻一階系統,傳遞函數的幅值近似為單位1,負的相移與頻率近似成線性關系。群延時只與時間常數有關,也就是說,極點會貢獻有限的相移。比如頻率比極點頻率低10倍頻的頻率點,極點會貢獻約-5.7度的相移。如果負的相移過大,就會引起系統振蕩。
三:一階系統階躍短時輸出響應
接下來,我們研究一下當一階系統發生階躍響應后,在起始很短一段時間內(遠小于一階系統時間常數τ)的輸出是什么樣子的。因為這一結論在實際工程應用中更為常見。

我們可以借用指數函數的展開式進行近似計算,由

我們可以得到:
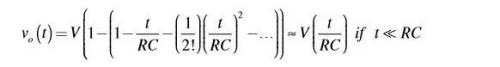
因此,在階躍響應發生后很短一段時間內,電壓看上去隨時間是線性變化的。由此可以推出流過電容的電流近似是恒定的:

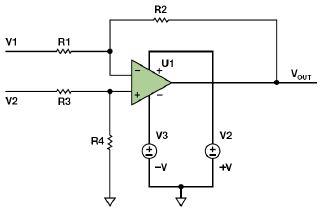
下面我們就用以上結論分析全橋整流系統的紋波電壓。一全橋整流系統如下:
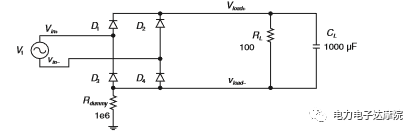
此系統輸入為120VRMS/60Hz的正弦波,RC時間常數為(100ohm)(1000uF)=100ms,遠遠大于輸入正弦波整流后饅頭波的周期8.3ms(1/120Hz)。因此我們利用上述結論可以比較容易算出電容上的紋波電壓:
輸出電壓最大值近似為170V;
流過100ohm電阻的電流近似為常數170V/100ohm=1.7A
電容會以8.3ms的時間常數進行放電來維持電阻上的電流(此時整流橋四個二極管全部關閉)
由I=Cdv/dt,我們就可以得到電容上的紋波電壓為:
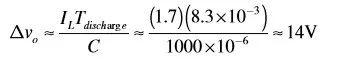
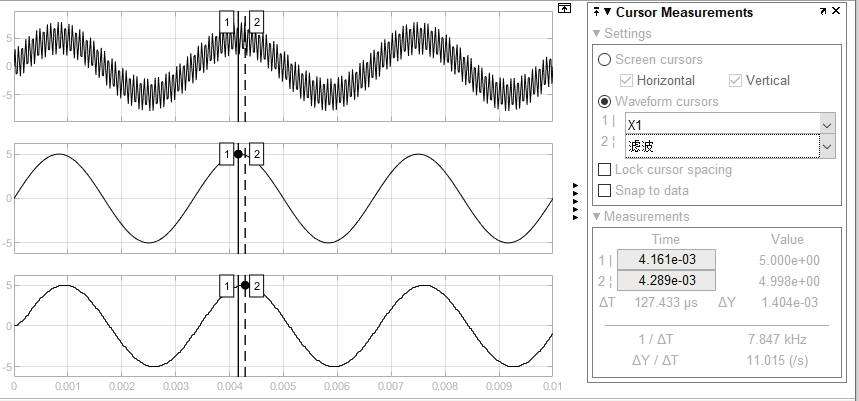
利用LTspice或者Pspice仿真軟件,我們可以得到這一結果:

接下來會簡單介紹二階系統。



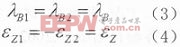
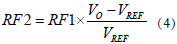
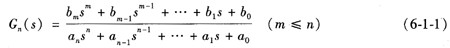
評論