基于半周期積分算法的微小振動測量研究

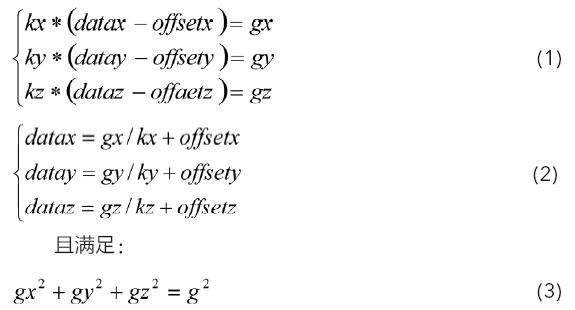
　　將式(1)、(2)、(3)整理，得到下面等式：

　　在對傳感器進行標定后，我們不能對加速度直接進行二重積分，那樣會將累積誤差無限放大。

　　根據單頻率振動的特點，我們分別對速度波形和振幅波形的繪制采用半周期積分法。這樣就可以在消除累積誤差的情況下，很好地繪制出振動軌跡。

2.5 半周期積分法^[8]

　　振動點在應力作用下，在平衡位置附近做往復運動。在振動點偏離平衡位置最大處，恰好是所測加速度值的一個極值點，也是速度值的零點;在振動點的平衡位置，則是加速度值的零點，是速度值的極值點。

　　根據以上特點，在對振動數據的加速度值進行處理時，我們采用半周期積分法，即從一個極值點積分到相鄰的下一個極值點，然后積分值歸零，再進行下一次積分。

　　例如，在由材料內部應力作用下而產生的振動情況中，對加速度從一個極大值點積分到下一個極小值點，對應的速度為從零點經過該速度的一個極大值點到下一個零點;對速度從一個極大值點積分到下一個極小值點，對應的振幅為從零點經過該振幅的一個極大值點到下一個零點。

3 結果檢驗與分析

3.1 單一頻率振動軌跡繪制

　　為了驗證系統的可靠性以及算法的優化程度，我們將對一個初始振動幅度為4mm的鐘擺式振動進行軌跡繪制。

3.2 結果分析

　　圖3是一個振動頻率為19Hz、初始振幅為4mm的鐘擺式振動加速度。

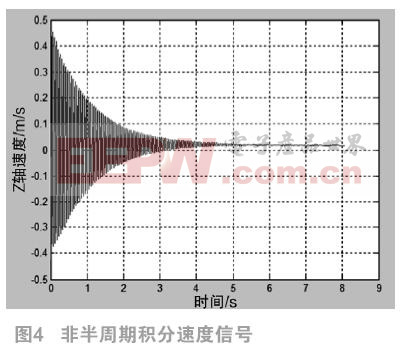
　　圖4和圖5分別是直接積分和采用半周期積分法得來的速度曲線。

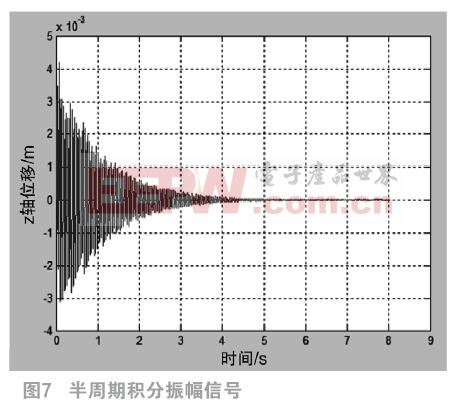
　　圖6和圖7分別是直接積分和采用半周期積分法得來的振幅曲線。

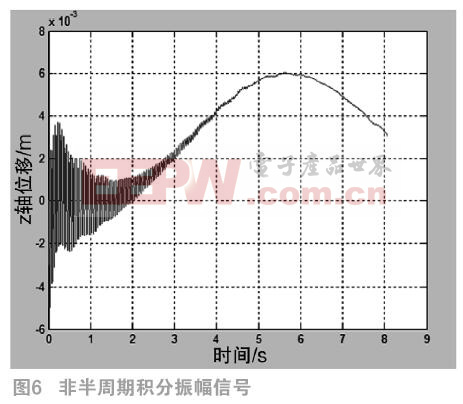
　　由圖4可以看出其有一個由累積積分誤差引起的直流偏置分量^[9]，圖6可以看出其由原始加速度經過二次積分對振幅帶來的災難性影響。

　　圖7可以看出其最終描繪出的初始振幅第一個極大值點為3.453mm，第二個極大值點為4.206mm，該現象的產生來自于算法的精度誤差。由于其初始值的最大幅度為4mm，其采樣點之間的差值會比較大，導致最終積分結果有比較明顯的差異。在振幅下降到1mm左右的時候，可以看出該算法精度誤差^[10]影響就很小了。

4 結論

　　本文提出了一種處理振動加速度數據的新型算法——半周期積分法，該算法明顯地降低了通過傳統積分算法而產生的累積的積分誤差，進而更加準確地描繪出了振動點的振幅波形。通過獲取該振幅波形一系列無量綱的幅值域參數，可以準確地判斷出機器的健康狀況。

　　本文在仿真驗證過程中，發現該算法對于振動點加速度數據采集的采樣頻率依賴性較高。對于振動幅值以及頻率較大的振動點，要求采樣頻率也要相應的提高，以此就可以獲得更加準確的振動波形。

　　參考文獻：

　　[1]嚴普強,喬陶鵬.工程中的低頻振動測量與其傳感器[J].振動、測試與診斷,2002,04:3-9+75.

　　[2]周東華,胡艷艷.動態系統的故障診斷技術[J].自動化學報, 2009, 35(6): 748-758.

　　[3]楊永波. 基于機器學習的故障狀態評價算法研究[D].遼寧大學,2013.

　　[4]孟小嵩.基于模式庫的礦山設備健康診斷方法研究[D].中國礦業大學,2014.

　　[5]袁小宏,屈梁生.機器振動診斷中信號處理方法的研究[J].西安交通大學學報,2001,07:714-717+730.

　　[6]齊國清.幾種基于FFT的頻率估計方法精度分析[J].振動工程學報,2006,01:86-92.

　　[7]張文瑞,張丕狀,翟子雄.一種基于六姿態模型的加速度計校準方法研究[J].傳感器與微系統,2016,03:37-39+48.

　　[8]SUN Yang, HUANG Jia dong, CHEN Da Zhuang. Novel Theory of Identifying Inrush Current Based on Half-cycle Sine Waveform[A]. Intelligent Information Technology Application Research Association (IITA Association), Hong Kong:,2010:4.

　　[9]Haiyong Wang, Min Lin, Yongming Li. A novel dynamic DC-offset canceller[A]. International Conference on ASIC Proceedings Book 1 of 2[C].Chinese Institute of Electronics(CIE):,2003:4.

　　[10]HUANG Qiang, ZHANG Gen bao. Precision Design for Machine Tool Based on Error Prediction[J]. Chinese Journal of Mechanical Engineering,2013,v.2601:151-157.

本文來源于《電子產品世界》2017年第4期第47頁，歡迎您寫論文時引用，并注明出處。