基于ANFIS的溫濕度控制
溫濕度控制現如今已經廣泛應用于人們的生產和生活中,如何能夠準確的控制這兩個變量一直是人們研究的問題。傳統的方法是通過溫度計、濕度計測量數據然后人為操作儀器升溫、加濕、通風、降溫和除濕,這種方法不僅精確度低、實時性效果差,而且對于操縱人員的要求高、勞動強度大,并且浪費時間和人力。現在采用的是智能化的檢測與控制,不但精度和實時性有所提高,而且操作簡便。如何能夠準確實時的將系統控制在理想的范圍是人們一直研究的問題和努力的目標。
本文引用地址:http://www.104case.com/article/201610/308702.htm如今照明行業的LED燈越來越多,高品質的燈需要經過嚴格的實驗測試才能達到5萬小時以上的照明時間,其中就包括在溫濕度環境的燒機實驗。本文主要介紹ANFIS,然后將該系統應用到LED溫濕度環境的測試控制中。
1 ANFIS的結構
Takagi和Sugeno在1985年提出了一種新的模糊推理模型,稱為Takagi—Sugeno(T—S)模型。該系統模型可使用極少數的模糊規則生成較繁雜龐大的非線性函數,具有計算效率高、輸出連續性、不但能夠將線性系統理論知識很好的結合而且非常適合數學分析的特點。自適應神經網絡模糊推理系統由T—S型模糊推理系統與人工神經網絡相結合,該系統具有模糊推理系統和人工神經網絡各自的優點,其最大的特點是根據已知數據就可以對控制系統進行建模,因此可以不需要事先知道被控系統的系統特性,或者對于系統特性比較復雜以及系統特性不明顯的控制系統,選用ANFIS往往能夠得到比傳統的控制方法更好的結果。
根據以上分析,論文采用基于T—S型模糊推理系統。該系統具有強大的自學習能力和非線性外推特性,其本質是通過學習訓練數據來實現輸入變量到輸出變量的線性或非線性映射,并在得出該映射關系后給出輸出變量的估計值。
圖1是一個典型的基于T—S型模糊神經推理系統的兩個輸入和一個輸出的ANFIS的結構圖。一共分為5層。
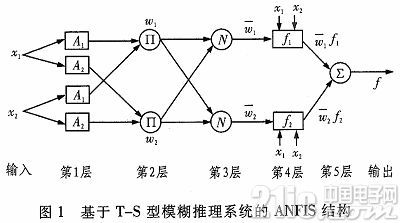
第1層:本層為條件參數。該層的每一個節點都是一個有節點函數的自適應節點,該層的節點函數是模糊集合的隸屬度函數,由它確定輸入x1(或x2)滿足論域A的程度。
Oij=μAji(xj),i=1,2;j=1,2
論域A的隸屬度函數包括高斯函數、三角函數和鐘型函數等,可以是任意一種合適的參數化的隸屬度函數。下式給出的是gauss隸屬度函數的表達式:

2 自適應模糊神經網絡的控制算法
減法聚類是一種密度聚類的算法。它是估計一組數據中聚類中心位置和聚類個數的快速的單次算法。減法聚類中每一個數據點都視為潛在的聚類中心,然后依據每個數據點周圍數據的密集程度來計算該點被當做聚類中心的可能性。其實現過程如下。
1)計算各個數據點的密度情況。對于m維空間的n個數據點(x1,x2,…,xn),我們認為每一個數據點都可能是聚類中心的候選者,于是各個數據點xi處的密度目標定義為:
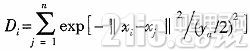
其中,ya是一個正數并且定義了一個鄰域數據點。
2)第1個聚類中心是選取具備最高密度目標的數據點,并且依此修正每一個需要作為聚類中心數據點的密度目標。令Dc為其密度目標,xc為選中的點,則每個數據點xi的密度目標可以通過下式修正,即
其中,yb是一個正數。由上所述靠近第1個聚類中心xc1的數據點密度目標會不斷減少,因此作為下一個聚類中心這些點是不可能的。
3)選定下一個聚類中心xc2一再次修正數據點的所有密度目標。
重復上述過程,如果上式達到最小值,則聚類結束。
減法聚類是以密度為聚類的算法,它應用于一個輸入、輸出數據集,依據數據集的聚類集個數和聚類中心的位置,能夠實現將輸入空間得到最優的劃分,并且確定輸入以及輸出語言變量的隸屬度函數的個數和模糊規則數。本文首先通過減法聚類得到最初始的模糊推理系統,再通過輸入輸出數據對系統進行進一步的優化,最終得到一個很合理的模糊推理系統。
3 ANFIS的參數學習方法
由自適應神經模糊推理系統中所涉及的參數一般都比較多,故對于ANFIS的條件參數和結論參數的訓練和確定,必須采用一種高效的參數學習方法。本文選用一種“混合算法”,該方法由Jang最早提出的,條件參數的修正使用反向傳播,結論參數修正選用線性最小二乘估計算法。其目的是為了提高ANFIS訓練數據學習的速度,盡可能快地確定最優的系統參數值,最終使得系統輸出結果的誤差平方和最小。
混合學習算法的整個學習過程如表1所示。
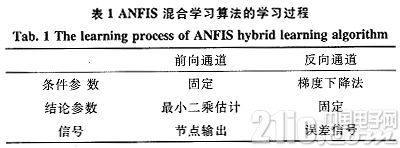
模糊神經網絡的學習算法是通過2步組成:首先將條件參數固定,輸入信號沿著網絡正向傳送至第4層,選用最小二乘法算法預估后件參數,信號繼續正向傳送至第5層輸出層;然后將得到的誤差信號沿著通道反向傳播,使用BP算法調整條件參數。這樣通過梯度下降法不但可以降低搜索空間的維數,還可以很好的提升參數的收斂速度。
本網絡系統中需要考慮的學習參數主要是條件參數{mji,σji}和結論參數{aji,j==0,1,2;i=1,2}。
定義目標函數為
式中:d為系統期望輸出或者教師信號。
誤差信號由第5層依次反向傳遞至第1層,具體算法:

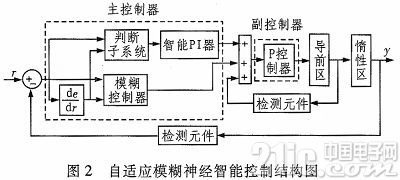
4 自適應模糊神經控制器設計
圖2為根據自適應模糊神經網絡控制的控制器,此控制器不但保持了常規串級控制,而且采用主、副控制器。主控制器使用一個模糊神經控制器和一個智能PI控制器來控制系統,副控制器仍然采用P控制器。
輸入變量的線性組合為自適應模糊神經系統的模糊規則,即:
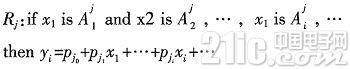
式中:i=1,2,…,n;j=1,2,…,m;Rj為第j條模糊規則所表示的模糊蘊含關系;![]() 為xj的第j個語言變量值,pj的后件網絡的連接權值。如果輸入量使用單個模糊化的方法,則對于系統給定的輸入x,可以求得關于每條規則的適應度為
為xj的第j個語言變量值,pj的后件網絡的連接權值。如果輸入量使用單個模糊化的方法,則對于系統給定的輸入x,可以求得關于每條規則的適應度為
![]()
式中:
是第i個輸入分量隸屬于第j個語言變量模糊集合A的隸屬度函數。
模糊系統的輸出量為每條規則的輸出量的加權平均,即
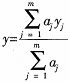
aj為對于給定的輸入x所求得的對于每條規則的適應度。
智能比例積分(PI)控制器是具有PI環節和使能端的邏輯判斷子系統的2個模塊組成。系統所處的狀態通過邏輯判斷子系統和的符號來判斷,從而控制P1環節是否有效。定義誤差e=r-y,誤差變化率ec,當e·ec>0或e=0、ec≠0時,PI控制器功能有效,主控制器由模糊神經網絡控制器和PI控制器共同作用控制實現,而當e·ec0或ec=0時,PI控制器功能失效,主控制器模塊由模糊神經網絡控制器單獨來控制。結合經驗知識,在仿真過程中通過對系統調試,最后確定的參數kp=1.2,ki=100。
5 ANFIS的仿真結果
溫度的偏差e和偏差變化率ec(濕度的偏差e和偏差變化率ec)為控制器的兩個輸入變量,E、EC為其對應的模糊化變量,[-6,+6]為E和EC的基本論域。通過查詢常規溫度模糊控制系統的訓練樣本表格和數據,神經模糊推理編輯器將訓練所得到的樣本數據載入訓練數據集,7定義為輸入變量的隸屬度函數的數目,類型為高斯型,輸出變量的隸屬度函數
類型為常數型.假設訓練的最初步長為0.01,目的誤差為0,最后模糊推理系統經過400步訓練后生成。為了形成對比本文對常規PID控制器和本文所研究的自適應模糊神經網絡控制器,在無外界擾動和有外界擾動的兩種情況下,進行了仿真,仿真結果見圖3和圖4。
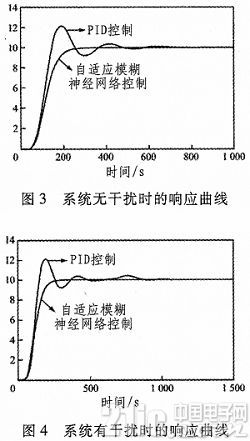
從圖片的結果可以看出,自適應模糊神經網絡控制器擁有良好的動、靜態特性和抗干擾能力,同時該控制器性能明顯比常規PID控制器要好,實現起來比傳統的PID控制簡單且基本沒有超調。
6 實際應用
本文采用Sensirion公司的SHT75溫濕度傳感器,該產品是該公司推出的一種插針式同時具有高精度版本的溫濕度傳感器。SHT75經過完全標定,傳感器具有高質量以及能夠提供高精度數字輸出。同時該產品是80uW的低能耗,相對溫度工作范圍:-40~+125℃,具有±0.3℃的精度。濕度工作范圍:0~100%,具有±1.8%RH的精度。
該控制器在現場使用時,根據SHT75測量的溫度值,反饋到系統顯示界面,根據反饋的數值決定設備是工作還是不工作。最終了解到隨著時間的不斷延長,自適應模糊神經網絡控制能夠將該系統的溫度維持在一個比較理想的范圍內。
7 結論
針對溫濕度控制系統存在的延時時間長、慣性強等特點,本文所研究的自適應模糊神經網絡的控制方法不僅克服了常規PID控制具有的自適應能力差的缺點,而且本文采用的模糊控制器解決了常規的模糊控制器存在的穩態精確度低和模糊系統規則難以把握等缺點。該控制方法不僅僅對于本文提出的溫濕度控制系統有效,同時對于復雜的被控對象也能取得比較好的控制效果,能夠展現出比較好的系統穩定性、抗外界干擾性和系統動態特性等優點,具有較高的工程應用價值。





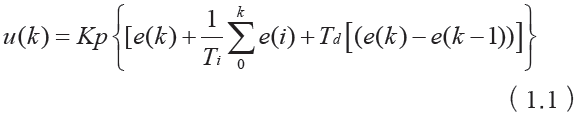
評論