一種處理金屬和介質混合結構連接邊界的新方法
(3)介質磁公共邊。在這些公共邊上定義介質面磁流密度,包含所有的介質面內部公共邊,未知數為Nj。在以上定義中,在連接邊界上只定義了面電流,面磁流不存在,并將面電流歸人介質面電流一類中,這樣在積分方程(11)~(14)可作為Jd統一處理。最終得到的滿秩阻抗矩陣維數為(2Nc+2Nd+Nj)×(2Nc+2Nd+Nj),而文獻[6]和文獻[8]中得到的初始的非滿秩矩陣維數分別為[Nc+2(Nc+Nj+Nd)]×[Nc+2(Nc+Nj+Nd)]和(2Nc+2Nd+4Nj)×(2Nc+2Nd+4Nj)。本文引用地址:http://www.104case.com/article/195688.htm
3 數值結果
計算一個位于自由空間中的圓柱、圓錐組合目標的雷達散射截面,剖分模型如圖3所示。
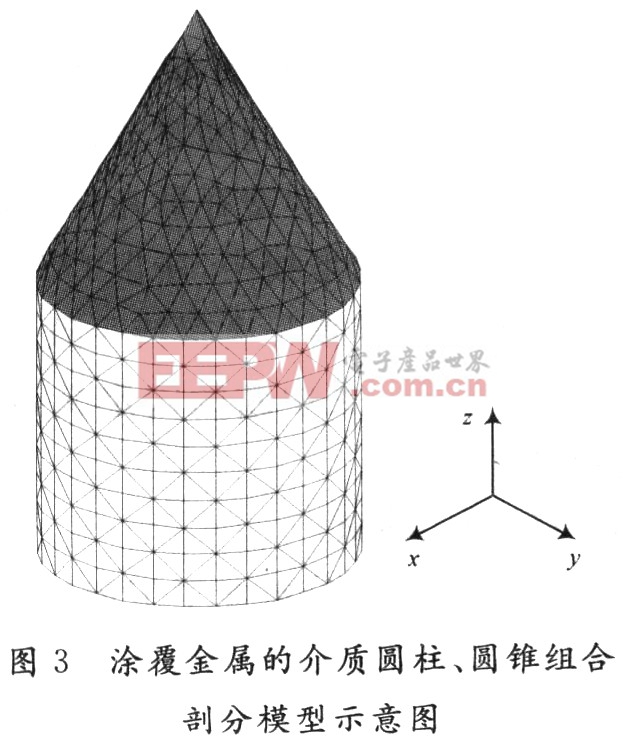
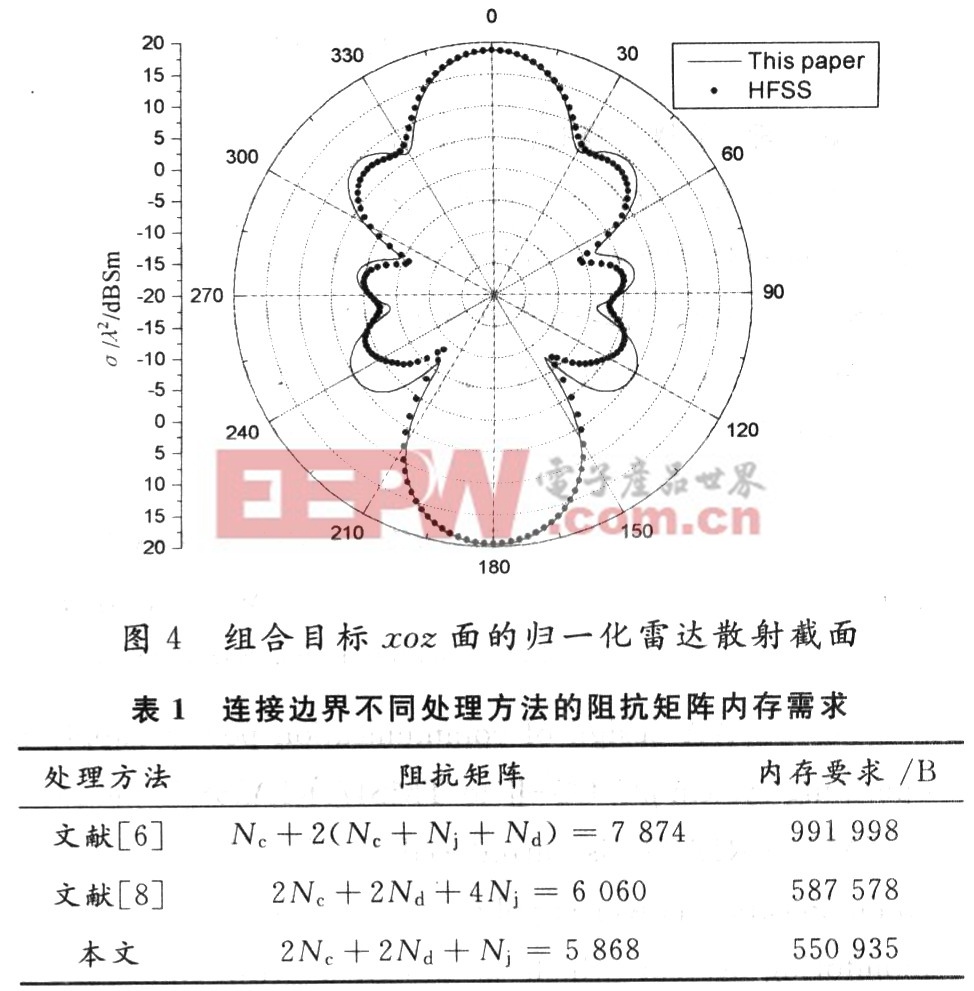
圓柱和圓錐的底面半徑和高分別為0.5λ,λ,目標的總高度為2λ。圓柱的下底面圓心位于坐標原點處。整個組合目標是εr=4.0,μr=1.0的均勻介質體,在圓錐面和圓柱下底面涂覆有理想金屬。此模型中,Nc=1 942,Nd=960,Nj=64。平面波入射方向為k=-z,極化方向E0=x。xoz面內的歸一化雷達散射截面如圖4所示。表1給出了連接邊界不同處理方法時,雙精度阻抗矩陣的內存需求,可以看出本文提出的方法所需內存最少。同文獻[8]的方法相比,雖然內存需求相差不多,但本文方法在得到阻抗矩陣后,不需要消去非獨立的變量,因而數值實現更為簡單。
4 結 語
本文根據連接邊界處的介質面元和金屬面元上的電流連續性和場的連續性,將定義在連接邊界公共邊上的電流歸入介質面電流,在積分方程中不需要給予額外的處理。另外,可用傳統的RWG基函數展開,不需要引入半個三角基函數,有效地減小了對計算機資源的需求,降低了計算復雜度,數值結果顯示了本文方法的正確性。







評論