一種處理金屬和介質(zhì)混合結(jié)構(gòu)連接邊界的新方法
0 引言
由金屬和均勻介質(zhì)組成的混合結(jié)構(gòu)在雷達散射、天線、微波工程等眾多領(lǐng)域都有著廣泛的應(yīng)用。采用矩量法求解由此類問題得到的表面積分方程,是一種廣泛而行之有效的數(shù)值分析方法。應(yīng)用等效原理,介質(zhì)散射問題可以等效為均勻媒質(zhì)中的外問題和內(nèi)問題進行分析。最早由Harrington等人給出介質(zhì)散射體的混合場積分方程,而Umashankar等則給出了任意形狀介質(zhì)散射體的RWG矩量法求解過程。Medgyesi-Mitschang等人提出的廣義矩量法能夠適用多種介質(zhì)構(gòu)成的混合結(jié)構(gòu)。該方法在不同介質(zhì)區(qū)域內(nèi)的邊界表面兩側(cè)分別引入電流層和磁流層,得到廣義的阻抗矩陣,通過聯(lián)系邊界表面兩側(cè)未知電流、磁流的關(guān)系來消去非獨立的方程組。這樣的處理方法具有一般性,且數(shù)值實現(xiàn)性好,但是需要占用更多的計算機資源。
對于介質(zhì)體涂覆有理想金屬面的混合結(jié)構(gòu),一個關(guān)鍵問題就是如何處理介質(zhì)表面和金屬表面的連接邊界。在最早Sarkar等人分析此類問題時,將金屬面視為可無限接近介質(zhì)體,但并不接觸,這實際是分離的金屬和介質(zhì)結(jié)構(gòu)的一種極限情況。這意味著在與金屬面重合的部分介質(zhì)表面,該模型需要引入一電流層和磁流層,這樣會增加待求解的未知數(shù)個數(shù),因此僅適用于相對簡單、電尺寸小的結(jié)構(gòu)。Su等人在分析二維混合問題時,忽略了跨過金屬面和介質(zhì)面之間的電流。Medgyesi-Mitschang等人給出了處理連接邊界的方法,在連接邊界處用半個三角基函數(shù)展開電流。根據(jù)電流連續(xù)性,令適當?shù)奈粗獢?shù)相等來消去一些方程,得到滿秩的矩陣方程。然而,在最初的矩陣填充過程中,必須首先得到非滿秩的矩陣方程。另外,對于連接邊界半個三角基函數(shù)需要給予特殊處理。Yla-Oijala等人給出了基于RWG基函數(shù)的介質(zhì)、金屬混合結(jié)構(gòu)的不同類型連接邊界的處理方法,仍采用在不同介質(zhì)區(qū)域內(nèi)的連接邊界表面兩側(cè)分別引入電流層和磁流層,通過聯(lián)系邊界表面兩側(cè)未知電流、磁流的關(guān)系來消去非獨立的方程組。文獻[11]給出了金屬介質(zhì)混合目標的體積分方程矩量法,該方法適合于非均勻介質(zhì)目標,對于均勻介質(zhì)目標來講,未知數(shù)與計算量會顯著增加。
本文給出一種處理金屬和介質(zhì)混合結(jié)構(gòu)連接邊界的新方法。在對模型表面進行三角面元近似后,根據(jù)電流連續(xù)性和電場、磁場連續(xù)性關(guān)系,連接邊界處的金屬面元上的電流與介質(zhì)面元上的電流呈現(xiàn)相同的特性。這樣的一對三角形仍可定義傳統(tǒng)的RWG基函數(shù),并在積分方程中歸入介質(zhì)電流統(tǒng)一進行處理,而且最初生成的阻抗矩陣即為滿秩的阻抗矩陣。
1 表面積分方程
考慮一個位于自由空間中的均勻介質(zhì)體,介質(zhì)體的部分外表面覆有理想金屬表面,如圖1所示。自由空間區(qū)域為R1,媒質(zhì)參數(shù)為ε1,μ1,σ1;介質(zhì)區(qū)域為R2,媒質(zhì)參數(shù)為ε2,μ2,σ2。圖中實線表示金屬面,虛線表示介質(zhì)面。根據(jù)表面等效原理,可以將此問題等效為如圖1(a),圖1(b)的外問
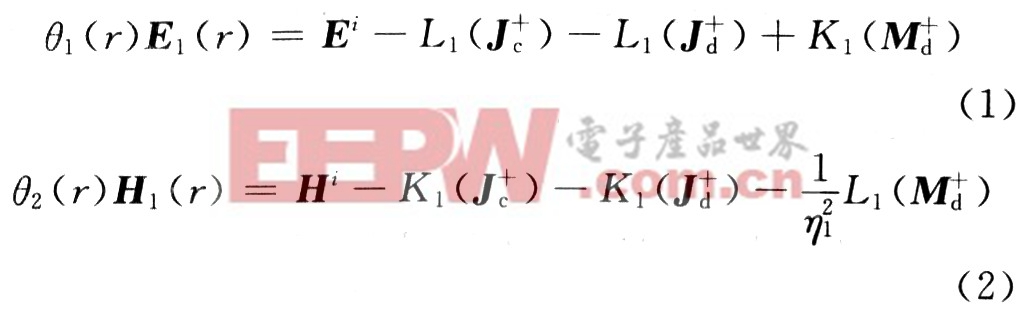
式中:θ1(r)為Heaviside函數(shù)來保證邊界處的階越條件。







評論