數(shù)頻率校正的FPGA實現(xiàn)

O 引言
在無線電接收機系統(tǒng)中，由于會受到發(fā)射機運動、接收機運動和標準頻率隨時間動態(tài)變化等因素的影響，其接收機接收信號往往會發(fā)生頻率偏移，因而需要進行頻偏校正。在擴頻通信系統(tǒng)中，頻偏校正電路能消除中頻偏移對接收機擴頻碼的捕獲以及數(shù)據(jù)解調(diào)性能的影響，從而提高接收機的性能。
頻偏校正電路中通常需要根據(jù)給定相位產(chǎn)生余弦信號和正弦信號，其中最重要的實現(xiàn)技術(shù)是CORDIC (Coordinate Rotation Digital Computer，坐標旋轉(zhuǎn)數(shù)字計算機)算法。本文將詳細分析CORDIC算法的原理及其FPGA實現(xiàn)方法。

1 CORDIC算法的基本原理
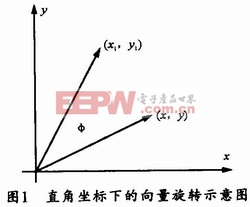
在直角坐標系統(tǒng)中，假設(shè)有一向量(x，y)，按逆時針方向旋轉(zhuǎn)φ度得到向量(x1，y1)，則兩向量的代數(shù)關(guān)系為：

在式(1)中，如果讓旋轉(zhuǎn)的角度φ滿足條件：tanφ=±2-i，則式(1)中的乘法操作就可以轉(zhuǎn)換為移位操作，從而很容易在FPGA中實現(xiàn)。圖l所示是直角坐標下的向量旋轉(zhuǎn)示意圖。若需要旋轉(zhuǎn)的角度為θ，那么就可以通過n次旋轉(zhuǎn)一系列預(yù)定角度αi來完成。

(2)式中，di表示每次旋轉(zhuǎn)的方向為αi。由于每次旋轉(zhuǎn)都為預(yù)定角度值，所以cosαi為常數(shù)，而n次旋轉(zhuǎn)中每次迭代的處理可表示為：


一般情況下，當旋轉(zhuǎn)的次數(shù)足夠大時，Ki一般為常數(shù)。由于在實現(xiàn)時，可在最終的計算結(jié)果中再乘以這一常數(shù)，所以，可以去掉式(3)中的Ki，這樣，迭代方程就僅含移位和加法運算，從而大大的簡化了FPGA的實現(xiàn)復(fù)雜性。由于還需要一個方程決定di的符號，引入變量zi表示每次旋轉(zhuǎn)預(yù)定角度的累加值：

這樣，CORDIC算法的迭代方程可表示為：

其最終結(jié)果為：

在頻偏校正電路中，通常需要根據(jù)給定相位θ產(chǎn)生余弦信號cosθ和正弦信號sinθ。為了產(chǎn)生標準且無放大的正弦和余弦信號，可令輸入向量的y分量(即yo)為0，x分量(即xo)為1／An，這樣，式(6)就可簡化為：

可見，經(jīng)過上述處理就可將輸入相位zo轉(zhuǎn)換為標準的正弦和余弦信號。