基于Nios的FFT算法軟硬件協同設計
由此可以看到,一個N點DFT已分解成2個N/2點的DFT。這2個N/2點的DFT再按照式(4)組合成1個N點DFT。這里應該看到 X1(k),X2(k)只有N/2個點,即k=O,1,…,(N/2)-1。而X(k)卻有N個點,即k=O,1,…,N-1,故用式(4)計算得到的只 是X(k)的前一半的結果,要用X1(k),X2(k)來表達全部的X(k)值,還必須應用系數的周期性,這樣可得到:

說明后半部分k值(N/2≤k≤N-1)所對應的X1(k),X2(k)分別等于前半部分k值(O≤k≤(N/2)-1)所對應的X1(k),X2(k)。這樣,就可將X(k)表達為前后兩部分:
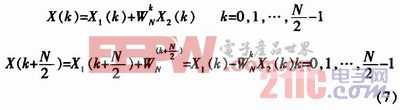
其運算關系可以利用蝶形運算流程圖來形象地描述,圖l為按時間抽取法的蝶形運算流程圖符號。本文引用地址:http://www.104case.com/article/191448.htm
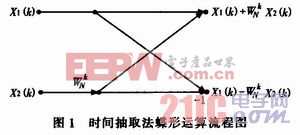
1.2 按頻率抽取的基-2FFT算法
仍設序列點數為N=2M,M為正整數。在把輸出X(k)按k的奇偶分組之前,先把輸入序列按前、后各一半(不是按偶奇)分開,把N點DFT寫成2部分,則可將DFT化為:






評論