基于FPGA的WALLACE TREE乘法器設計
摘要:為了使基于FPGA設計的信號處理系統具有更高運行速度和具有更優化的電路版圖布局布線,提出了一種適用于FPGA結構的改進型WALLACE TREE架構乘法器。首先討論了基于標準單元3:2壓縮器的改進型6:4壓縮器,根據FPGA中slice的結構特點通過在FPGA Editer軟件工具編輯,對該壓縮器進行邏輯優化,將其應用于FPGA的基本單元slice結構中。并對乘法器的其他部分結構優化整合,實現一個資源和性能達到合理平衡,且易于在FPGA中實現的乘法器。實際運行結果表明,該乘法器的關鍵路徑延時小于8.4 ns,使乘法器時鐘頻率和系統性能都得到很大提高。
關鍵詞:乘法器;WALLACE;FPGA;6:4壓縮器
在數字信號處理中,乘法器是整個硬件電路時序的關鍵路徑。速度和面積的優化是乘法器設計過程的兩個主要考慮因素。由于現代可編程邏輯芯片FPGA的集成度越來越高,及其相對于ASIC設計難度較低和產品設計周期短,受到很多廠家和研究機構的關注。利用它的可編程和可擴展性,可將傳統乘法器設計方法應用到FPGA芯片中。乘法器設計基本上是部分積的生成及其之間的相加的優化過程。針對FPGA內部固有結構的特點,本文著重介紹了一種基于WALLACETREE優化算法的改進型乘法器架構。根據FPGA內部標準獨特slice單元,有必要對WALLACE TREE部分單元加以研究優化,從而讓在FPGA的乘法器設計中的關鍵路徑時延得以減小,整體時鐘性能得以提高。也能夠使FPGA的面積資源合理優化,提高器件的整體資源利用率。
1 WALLACE TREE結構
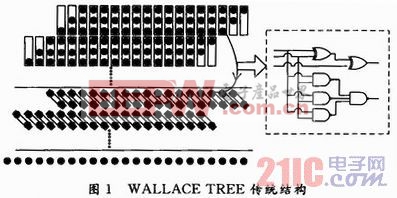
WALLACE TREE是對部分積規約,減小乘法器關鍵路徑時延的一種算法。傳統WALLACE TREE結構的CSA(Carry Save Adder)陣列乘法器如圖1所示,其中“·”代表生成的多個部分乘積項,相應電路中用邏輯與門來實現。求和陣列將前面生成的多個部分積通過3:2 CSA壓縮器,將其壓縮成2個部分積,最后通過末級進位相加得到所需的最終乘積結果。圖中矩形框所示為3:2 CSA壓縮器,其電路邏輯等效于一個全加器結構。通過運算可知N個部分積,要經類似的log(2N/3)級3:2壓縮,就可得到2個部分積。
2 壓縮器的優化
由于FPGA內部的結構是固定的,沒有以上WALLACE TREE所需要的CSA標準全加器結構。因此,在傳統的FPGA電路綜合實現時,該CSA全加
器被綜合在FPGA內部查找表(LUT)和進位鏈中,占用了整個slice單元的資源。由于經典WALLACETREE結構不具有良好的對稱性且需要權重對齊等因素,勢必要增大FPGA電路的復雜度,增加大量的FPGA內部布局和布線資源,在FPGA中不規則的布局布線結構,也增大了關鍵路徑的時延。
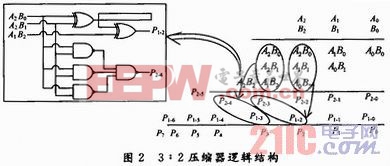
為在FPGA中較好地實現WALLACE TREE結構,結合FPGA中最小標準單元的結構silce,對CSA全加器單元結構加以改進。如圖2所示,可將WALLACE TREE相鄰的平級3:2 CSA壓縮器合并成一個6:4壓縮器。該壓縮器只需使用1個FPGA的silce資源,就能實現其數字邏輯。下面以3×3乘法器為例,進行WALLACE TREE壓縮器的推導和優化。如圖2的第一個部分積,部分積低位空白應補0,高位空白位用該部分積的最高位補齊。















評論