利用FFT IP Core實現FFT算法

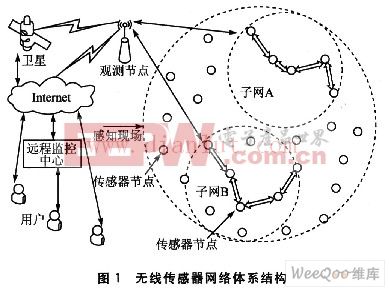
結合工程實踐，介紹了一種利用FFT IP Core實現FFT的方法，設計能同時對兩路實數序列進行256點FFT運算，并對轉換結果進行求模平方運算，且對數據具有連續處理的能力。設計采用低成本的FPGA實現，具有成本低、性能高、靈活性強、速度快等特點，而且通過工程應用證明了設計是正確可行的。

由于FFT(快速傅里葉變換)的問世，促進了數字信號處理這門學科的成熟，它可應用于傅里葉變換理論所能涉及的任何領域。FFT傳統實現

方法無非是軟件(軟件編程)和硬件(專用芯片ASIC)兩種，FPGA的出現使人們在FFT的實現方面又多了一種選擇。FPGA同時具有軟件編程的靈活性和ASIC電路的快速性等優點，適合高速數字信號處理。大多數FPGA廠商都提供了可配置的邏輯核(Core)實現各種算法功能，其中包括FFT IP Core(知識產權核)。使用這些資源允許設計師將更多的時間和精力放在改善增加系統功能上，這無疑將大大減少設計風險及縮短開發周期。

本設計采用了Altera公司的FFT IP Core實現FFT功能，可同時實現兩路256點實數數據的FFT轉換，并對轉換結果進行求模平方運算，設計對數據具有連續處理的能力。FPGA芯片選用的是有史以來成本最低的Altera公司的Cyclone系列的芯片，FFT內核是Altera MegaCore FFT-V2.0.0，整個設計成本低、性能好，已經成功地應用到雷達產品中。

2 算法原理和FFT Core介紹

設計用到的算法包括同時計算兩個實函數的FFT算法和CORDIC算法。

2.1 同時計算兩個實函數的FFT算法

DFT(離散傅里葉變換)的定義為：

式(1)中，都假定時間函數x(n)是一個復函數。但是在許多FFT的實際應用中，時間函數往往是實函數。下面介紹的算法可以有效地減少實數序列FFT的計算工作量，從而提高計算速度。該方法可歸納為如下幾個步驟：
①函數h(n)和g(n)是兩個實函數，n=0，1，…，N-1；
②將其中的一個作為實部而另一個作為虛部，構成復函數z(n)為：
z(n)=h(n)+jg(n)， n=0，1，…，N-1；
③計算z(n)的N點DFT得：

式中，H(k)和G(k)分別是h(n)和g(n)的DFT。

詳細的推導過程參見文獻[2]。

2.2 CORDIC算法原理

CORDIC(The Coordinate Rotational Digital Computer)算法是一種循環迭代算法，其基本思想是用一系列與運算基數相關角度的不斷偏擺從而逼近所需旋轉的角度。從廣義上講它是一個數值性計算逼近的方法，由于這些固定的角度與計算基數有關，運算只有移位和加減。可用該算法來計算的函數包括乘、除、平方根、正弦、余弦正切、向量旋轉(即復數乘法)以及指數運算等。CORDIC的基本原理如下。

向量x+jy，旋轉角度θ到向量x'+jy'，假設的方向用δ表示，旋轉的角度為θi，并且θi滿足關系：tanθi=2i。則由文獻[3]的推導可知:

2.3 FFT Core簡介

FFT-V2.0.0是Altera公司2004年2月新發布的FFT知識產權核，它是一個高性能、高度參數化的快速傅里葉變換(FFT)處理器，支持Cyclone、