航空電子設備PCB組件的動態分析
加入技術交流群
1.2 有限元模態分析結果
建立起對象PCB 組件的有限元模型，并采用蘭索斯分塊法(Block Lanczos Method)進行模態分析。模態分析就是通過求解系統的特征方程，一般多自由度系統的特征方程可以成式(1)所示的形式，來得到系統的特征值和特征向量，亦即振動系統固有頻率和振型。
式中，[M]-系統的質量矩陣，有限元模態分析中由單元質量矩陣組裝而成;[K]-系統的剛度矩陣，有限元模態分析中由單元剛度矩陣組裝而成;{X}—系統的位移向量;ω-系統的特征值。
通過模態分析，得到了采用四顆螺釘固定的對象PCB 組件的前三階固有頻率和振型，具體見表2。該PCB 組件的第1 階振型為一階彎曲，第2 階振型為扭轉，第3 階振型為正弦波狀彎曲。這些振型與得到的四顆螺釘固定下JEDEC 標準板相似。
表2 有限元模態分析結果
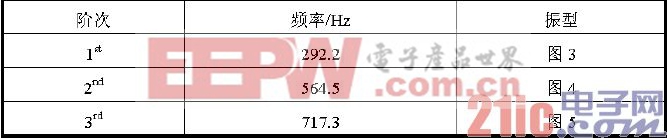
圖3 PCB 組件第1 階振型(FEA)
圖4 PCB 組件第2 階振型(FEA)
圖5 PCB 組件第3 階振型(FEA)
評論